2022-08-01

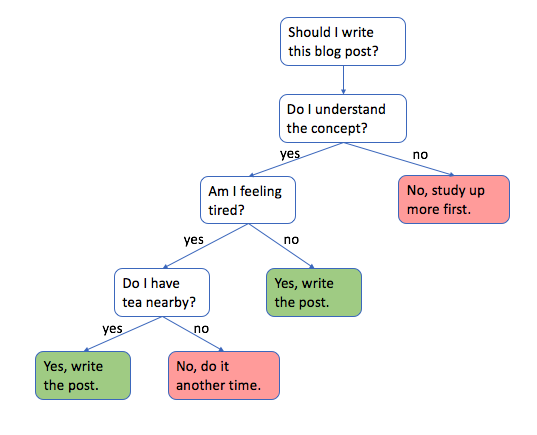
Apa itu Decision Tree

Apa itu Decision Tree

Decision tree adalah alat pemodelan prediksi yang kuat yang digunakan untuk menyelesaikan berbagai masalah klasifikasi dan regresi. Meskipun sederhana, keefektifan dan sifat visualnya memudahkan interpretasi dan komunikasi hasil.

Decision trees.

Decision tree adalah struktur seperti diagram alir di mana simpul internal mewakili fitur atau atribut, cabang mewakili aturan keputusan, dan simpul daun mewakili hasil atau keputusan. Pohon dibangun melalui proses yang disebut rekursif binary splitting, yang melibatkan pemilihan atribut terbaik untuk membagi dataset dan kemudian secara berulang mengulang proses pada subset yang dihasilkan hingga mencapai kriteria berhenti tertentu.

Decision tree dapat digunakan dalam berbagai aplikasi, seperti keuangan, kesehatan, pemasaran, dan deteksi kecurangan. Dengan memahami cara membangun, menginterpretasi, dan mengevaluasi decision tree, seseorang dapat membuat keputusan yang berdasarkan pola dan tren yang tersembunyi dalam data.

Membangun Decision Tree

Di bab ini, saya akan menjelajahi proses membangun decision tree, mulai dari konsep dasar rekursif binary splitting dan berkembang ke teknik lebih lanjut untuk memilih pemisahan terbaik dan memangkas pohon. Kita akan membahas berbagai ukuran ketidakmurnian, seperti indeks Gini dan entropi, dan bagaimana pengaruhnya pada proses konstruksi pohon.

Rekursif Binary Splitting

Rekursif binary splitting adalah metode utama yang digunakan untuk membangun decision tree. Proses ini melibatkan pembagian dataset menjadi subset berdasarkan nilai fitur masukan. Dimulai dengan simpul akar, yang berisi seluruh dataset, dan secara iteratif membagi data menjadi dua simpul anak dengan memilih atribut dan nilai ambang. Proses ini berlanjut secara rekursif untuk setiap simpul anak hingga memenuhi kriteria penghentian tertentu, menghasilkan struktur pohon dengan simpul keputusan dan simpul daun.

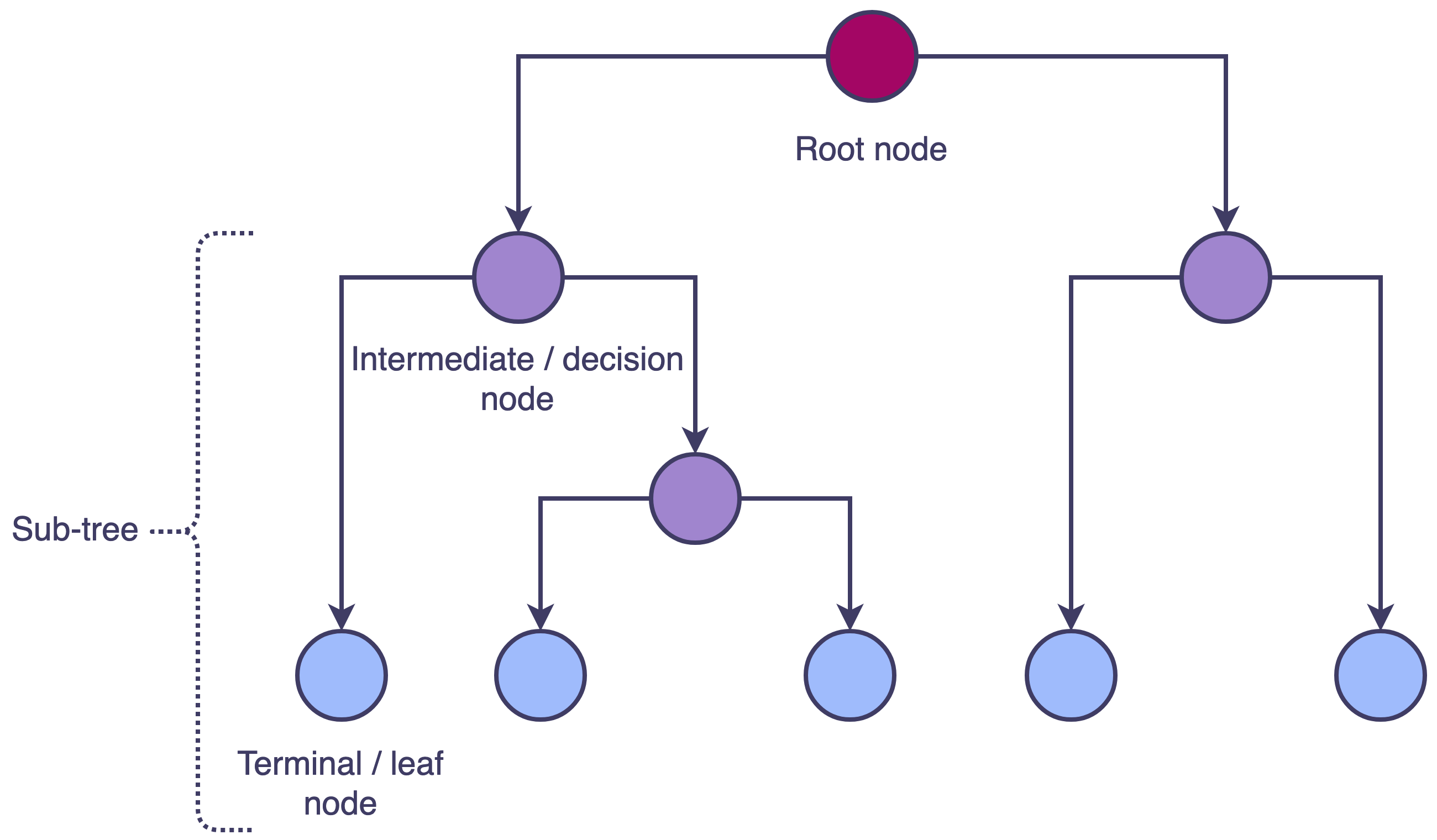
Tree splitting
An introduction to decision tree theory

Memilih Split Terbaik

Kualitas decision tree sangat bergantung pada pemilihan atribut dan nilai ambang yang digunakan untuk membagi data. Untuk memilih split terbaik, kita harus mengevaluasi potensi split dengan mengukur ketidakmurnian dari simpul anak yang dihasilkan. Tujuannya adalah untuk meminimalkan ketidakmurnian di simpul anak, dengan demikian memaksimalkan Information Gain yang dicapai melalui split.

Information Gain

Information Gain merupakan konsep kunci dalam pohon keputusan yang digunakan untuk menentukan atribut terbaik untuk membagi data pada setiap simpul. Information Gain mengukur pengurangan ketidakpastian atau keacakan setelah membagi data berdasarkan atribut tertentu. Information Gain dihitung menggunakan entropi, sebuah ukuran dari ketidakmurnian atau ketidakberaturan dalam sebuah kumpulan data.

Untuk menghitung Information Gain, entropi simpul induk dikurangi dengan entropi rata-rata terbobot dari simpul anak yang dibuat setelah pemisahan. Atribut dengan Information Gain tertinggi dipilih sebagai atribut pemisahan pada simpul tersebut. Proses ini diulangi untuk setiap simpul selanjutnya hingga pohon sepenuhnya tumbuh.

Information Gain = Entropi(induk) - Rata-rata Terbobot Entropi(anak)

IG(S, A) = H(S) - \sum_{v \in A} \frac{|S_v|}{|S|} H(S_v)

di mana $GI(S, A)$ adalah Information Gain untuk atribut $A$ , $H(S)$ adalah entropi dari kumpulan data $S$ , dan $H(S_v)$ adalah entropi dari subset $S_v$ .

Entropi

Entropi adalah ukuran ketidakmurnian atau ketidakberaturan dalam kumpulan data, digunakan terutama dalam konteks pohon keputusan dan teori informasi. Entropi mengukur ketidakpastian atau keacakan yang terkait dengan distribusi label kelas dalam sebuah kumpulan data. Dalam pohon keputusan, entropi digunakan untuk menghitung Information Gain, yang pada gilirannya membantu menentukan atribut terbaik untuk membagi data.

Entropi dihitung menggunakan rumus berikut:

Entropy(S) = - \sum_{i=1}^{c} p(i) * log_2(p(i))

di mana $Entropi(S)$ adalah entropi dari kumpulan data $S$ , $c$ adalah jumlah kelas, dan $p(i)$ adalah probabilitas sebuah instance termasuk dalam kelas $i$ . Entropi berkisar dari 0 hingga $log_2(c)$ , di mana $c$ adalah jumlah kelas. Nilai entropi yang lebih rendah menunjukkan kumpulan data yang lebih homogen, sedangkan nilai yang lebih tinggi mewakili kumpulan data yang lebih bercampur. Dalam pohon keputusan, tujuannya adalah untuk meminimalkan entropi pada setiap simpul, sehingga terjadi pemisahan kelas yang lebih jelas dan prediksi yang lebih akurat.

Indeks Gini

Indeks Gini, juga dikenal sebagai ketidakmurnian Gini atau koefisien Gini, adalah ukuran lain yang digunakan untuk menentukan atribut terbaik untuk membagi data dalam pohon keputusan. Indeks Gini mengukur ketidakmurnian atau ketidakberaturan dalam kumpulan data dan, seperti Information Gain, membantu mengidentifikasi atribut yang paling informatif untuk pemisahan.

Indeks Gini berkisar dari 0 hingga 1, dengan 0 mewakili kemurnian sempurna (semua instance di simpul termasuk dalam satu kelas) dan 1 mewakili ketidakmurnian maksimum (instance terdistribusi merata di semua kelas). Atribut dengan indeks Gini terendah dipilih sebagai atribut pemisahan pada simpul tertentu.

Gini(S) = 1 - \sum_{i=1}^{c} p(i)^2

di mana $Gini(S)$ adalah indeks Gini untuk kumpulan data $S$ , $c$ adalah jumlah kelas, dan $p(i)$ adalah probabilitas sebuah instance termasuk dalam kelas $i$ .

Memangkas Tree

Decision tree kadang-kadang dapat tumbuh terlalu besar, mengarah ke overfitting, yang berarti tree bekerja dengan baik pada data pelatihan tetapi buruk pada data baru yang belum terlihat. Memangkas adalah teknik yang digunakan untuk mengurangi ukuran tree dan mengurangi overfitting. Ada dua metode pruning utama: pre-pruning dan post-pruning.

Pre-pruning
Pre-pruning melibatkan pengaturan kriteria penghentian sebelum pohon sepenuhnya tumbuh, seperti membatasi kedalaman maksimum pohon atau mengharuskan jumlah sampel minimum dalam simpul daun.
Post-pruning
Post-pruning melibatkan pertumbuhan pohon sepenuhnya dan kemudian secara iteratif menghapus cabang yang tidak berkontribusi pada akurasi prediksi pohon. Teknik pruning yang paling umum adalah cost-complexity pruning, yang menyeimbangkan tingkat kesalahan dengan kompleksitas pohon.

Implementasi Decision Tree di Python

Di bab ini, saya akan menunjukkan cara mengimplementasikan classifier decision tree di Python menggunakan library machine learning Scikit-learn. Kita akan menggunakan dataset Iris sebagai contoh, yang merupakan masalah klasifikasi multikelas.

Persiapan Data

Sebelum membangun decision tree, penting untuk mempersiapkan dataset. Langkah ini melibatkan memuat data, membaginya menjadi set pelatihan dan pengujian, dan mungkin preprocessing data untuk menangani nilai yang hilang, variabel kategorikal, atau fitur scaling.

python

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

# Load dataset
iris = load_iris()
X = iris.data
y = iris.target

# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

Mendefinisikan Model

Selanjutnya, tentukan model decision tree menggunakan kelas DecisionTreeClassifier dari Scikit-learn. Kelas DecisionTreeClassifier memungkinkan Anda untuk menyesuaikan model dengan mengatur berbagai hiperparameter yang mengontrol pertumbuhan dan struktur pohon.

python

from sklearn.tree import DecisionTreeClassifier

# Define model
dtree = DecisionTreeClassifier(
  criterion='gini',
  max_depth=None,
  min_samples_split=2,
  min_samples_leaf=1,
  random_state=42
)

Berikut adalah penjelasan singkat dari hiperparameter utama:

criterion
Kriteria untuk mengukur ketidakmurnian simpul. Ini bisa jadi 'gini' untuk indeks Gini atau 'entropy' untuk entropy. Nilai default adalah 'gini'.
max_depth
Kedalaman maksimum pohon. Jika diatur ke None, pohon akan memperluas hingga semua daun murni atau berisi kurang dari min_samples_split sampel. Mengatur kedalaman maksimum dapat membantu mencegah overfitting.
min_samples_split
Jumlah sampel minimum yang diperlukan untuk membagi simpul internal. Jika simpul internal memiliki sampel kurang dari nilai ini, itu tidak akan dibagi, dan pertumbuhan pohon akan dihentikan. Nilai default adalah 2.
min_samples_leaf
Jumlah sampel minimum yang diperlukan untuk berada di simpul daun. Split hanya akan dipertimbangkan jika itu meninggalkan setidaknya sampel min_samples_leaf di setiap cabang kiri dan kanan. Hiperparameter ini dapat membantu mencegah overfitting dengan memastikan bahwa pohon tidak membuat simpul daun yang terlalu spesifik. Nilai default adalah 1.
random_state
Biji untuk generator nomor acak yang digunakan oleh algoritma. Dengan mengatur keadaan acak, Anda dapat memastikan bahwa model decision tree Anda dapat direproduksi. Jika diatur ke None, hasil model dapat bervariasi antara jalankan karena keacakan dalam proses pemecahan.

Melatih Model

Sekarang, latih model decision tree pada data pelatihan.

python

# Train model
dtree.fit(X_train, y_train)

Memprediksi

Gunakan model decision tree yang dilatih untuk memprediksi label kelas untuk data pengujian dan mengevaluasi kinerja model menggunakan metrik seperti akurasi, presisi, recall, dan F1-score.

python

from sklearn.metrics import classification_report, accuracy_score

# Predict
y_pred = dtree.predict(X_test)

# Evaluate model performance
print("Accuracy:", accuracy_score(y_test, y_pred))
print(classification_report(y_test, y_pred))

Accuracy: 1.0
              precision    recall  f1-score   support

           0       1.00      1.00      1.00        19
           1       1.00      1.00      1.00        13
           2       1.00      1.00      1.00        13

    accuracy                           1.00        45
   macro avg       1.00      1.00      1.00        45
weighted avg       1.00      1.00      1.00        45

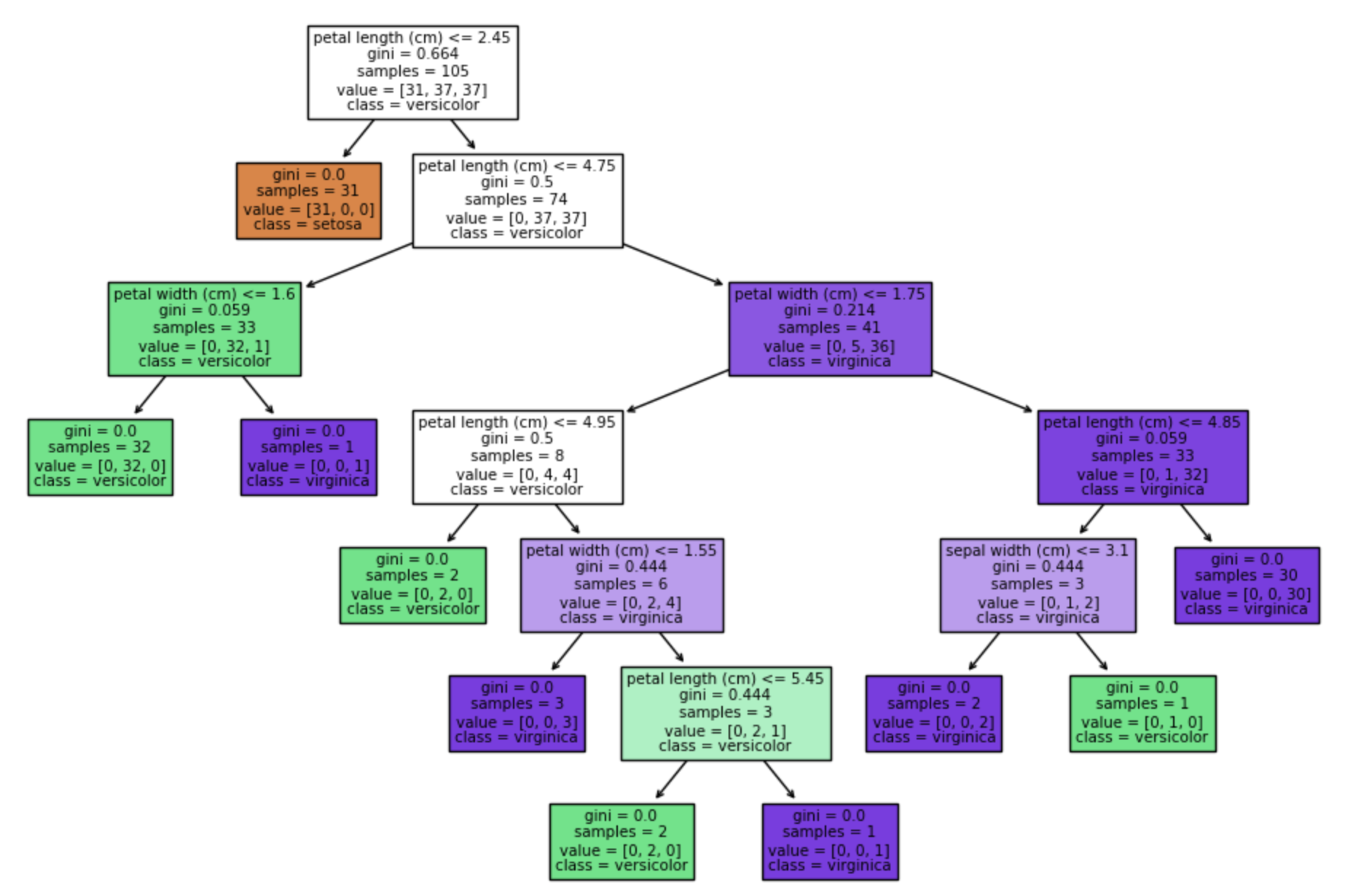
Visualisasi Decision Tree

Visualisasi decision tree dapat membantu Anda memahami bagaimana model membuat prediksi dan meningkatkan interpretabilitasnya. Anda dapat menggunakan fungsi plot_tree dari Scikit-learn untuk membuat representasi grafis dari decision tree.

python

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

# Visualize decision tree
plt.figure(figsize=(12, 8))
plot_tree(dtree, filled=True, feature_names=iris.feature_names, class_names=iris.target_names)
plt.show()