2022-11-04

Algoritme pengoptimalan

Apa itu algoritma optimasi?

Tujuan dari pelatihan neural network adalah untuk menemukan parameter yang meminimalkan nilai loss function sebanyak mungkin. Algoritma optimasi adalah algoritma untuk secara efisien sampai pada nilai minimum loss ini.

Algoritma optimasi sering dibandingkan dengan petualang. Idenya adalah untuk mencapai dasar lembah terdalam di area tanah yang luas dengan mata tertutup, tanpa melihat peta. Karena kita ditutup matanya, kita hanya mengandalkan kemiringan di bawah kaki kita untuk mencapai dasar lembah. Pemain harus merasakan kemiringan tanah dan menyusun strategi untuk mencapai dasar lembah. Jika strateginya tidak benar, Anda mungkin akan berakhir di depresi lokal atau mengambil jalan memutar untuk mencapai dasar lembah. Cara mencapai minimum yang benar secara efisien adalah penting.

Metode penurunan gradien

Metode gradient descent adalah metode diferensiasi fungsi kerugian dengan parameter, mencari arah untuk mengurangi kerugian, dan menyesuaikan parameter ke arah itu. Metode gradient descent mengulangi langkah-langkah berikut.

masukan data ke jaringan saraf dan prediksi keluaran
tentukan fungsi kerugian untuk nilai yang benar dan yang diprediksi
membedakan fungsi kerugian dengan parameter
perbarui parameter dengan nilai yang dibedakan

Langkah ini dapat dinyatakan dalam rumus matematika sebagai berikut.

w_{t+1} = w_t-\eta\frac{\partial L}{\partial w_t}

Di sini $w$ menunjukkan parameter untuk update $t$ ke-t, $L$ menunjukkan fungsi kerugian, $\frac{\partial L}{\partial w}$ adalah kemiringan fungsi kerugian sehubungan dengan $w$ , dan $\eta$ adalah hiperparameter yang disebut tingkat pembelajaran. Persamaan untuk memperbarui parameter disebut persamaan pembaruan.

Pembaruan parameter membutuhkan dua keputusan berikut

Apakah akan meningkatkan atau menurunkan nilai parameter
Berapa banyak perubahan nilai parameter

Yang pertama ditentukan oleh turunan dari gradien. Yang kedua ditentukan oleh laju pembelajaran.

Metode gradient descent bisa dibagi menjadi tiga jenis berikut ini, tergantung pada jumlah data yang digunakan

Gradien descent batch
SGD (Stochastic Gradient Descent)
SGD mini-batch

Gradient descent batch

Metode batch gradient descent mencari nilai minimum dari fungsi kerugian menggunakan semua data. Ini berarti bahwa metode batch gradient descent digunakan untuk rata-rata semua data.

Meskipun metode batch gradient descent dapat memperbarui parameter sekaligus, metode ini memiliki kelemahan sebagai berikut

Secara komputasi mahal.
Sulit untuk keluar ketika terjebak dalam solusi optimal lokal.

Di antara kerugiannya, jumlah komputasi yang besar dapat diselesaikan dengan komputasi paralel. Namun, tidak dapat dihindari bahwa ketika terjebak dalam solusi optimal lokal, tidak ada jalan keluar. Solusi optimal lokal adalah nilai minimum yang bukan minimum. Jika data yang sama digunakan untuk setiap pembaruan parameter, tidak mungkin untuk keluar dari optimal lokal setelah jatuh ke dalam minimum lokal karena data yang sama persis dimasukkan ke dalam optimal lokal. SGD memecahkan masalah ini.

SGD (PStochastic Gradient Descent)

SGD (Stochastic gradient descent) adalah algoritma yang secara acak memilih data untuk setiap pembaruan parameter. Sementara metode batch gradient descent menggunakan semua data untuk pembaruan parameter tunggal, SGD hanya menggunakan satu bagian data yang dipilih secara acak untuk setiap pembaruan. Oleh karena itu, SGD menghilangkan masalah konvergensi ke solusi optimal lokal yang dapat terjadi dalam metode batch gradient descent dengan memilih sampel secara acak untuk setiap pembaruan $ w $. Ini juga memiliki keuntungan belajar secara efisien dari redundansi dalam data pelatihan.

Salah satu kelemahan SGD adalah tidak dapat diparalelkan dan pembelajarannya lambat karena tidak dapat berpindah ke data berikutnya kecuali jika diperbarui dengan gradien dari satu set data.

SGD mini-batch

SGD mini-batch adalah metode antara SGD dan batch gradient descent. Metode ini menggunakan sebagian data untuk mencari nilai minimum dari fungsi loss.

Metode batch gradient descent menghitung gradien dari semua data, sehingga perhitungannya dapat diparalelkan. Di sisi lain, SGD tidak dapat memparalelkan komputasi karena jumlah data untuk komputasi gradien adalah satu. Oleh karena itu, mini-batch SGD, yang menggunakan jumlah data tetap untuk pelatihan, dapat mencapai paralelisasi sambil mempertahankan keacakan. Dengan kata lain, mini-batch SGD adalah metode yang berada di antara metode batch gradient descent dan SGD. Ukuran batch SGD mini-batch adalah hyper-parameter, seringkali 16 atau 32.

Namun, bahkan dengan SGD mini-batch, ada masalah bahwa ketika mencari nilai minimum dari fungsi kerugian, ia jatuh ke dalam depresi yang disebut kelengkungan patologis, menyebabkan overshooting (osilasi yang terjadi ketika pembaruan tunggal terlalu besar) dan pembelajaran yang lambat. Untuk mengilustrasikan masalah osilasi ini, pertimbangkan masalah mencari nilai minimum dari fungsi berikut.

f(x,y) = \frac{1}{20}x^2 + y^2

Fungsi ini berbentuk elips yang memanjang sepanjang sumbu $x$ . Gradien fungsi ini kecil di sepanjang sumbu $x$ - dan besar di sepanjang sumbu $y$ -. Nilai minimum dari fungsi ini adalah $(x, y) = (0,0)$ . Mulai pencarian dari $(x, y) = (-7,2)$ dan terapkan SGD. Kodenya adalah sebagai berikut.

import numpy as np
import matplotlib.pyplot as plt

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):
    return x / 10.0, 2.0*y

init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0

optimizer = SGD(lr=0.95)

x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]

for i in range(30):
    x_history.append(params['x'])
    y_history.append(params['y'])

    grads['x'], grads['y'] = df(params['x'], params['y'])
    optimizer.update(params, grads)

x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)

X, Y = np.meshgrid(x, y)
Z = f(X, Y)

# for simple contour line
mask = Z > 7
Z[mask] = 0

# plot
plt.figure(figsize=(12,6))
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
plt.title("SGD")
plt.xlabel("x")
plt.ylabel("y")

plt.show()

SGD

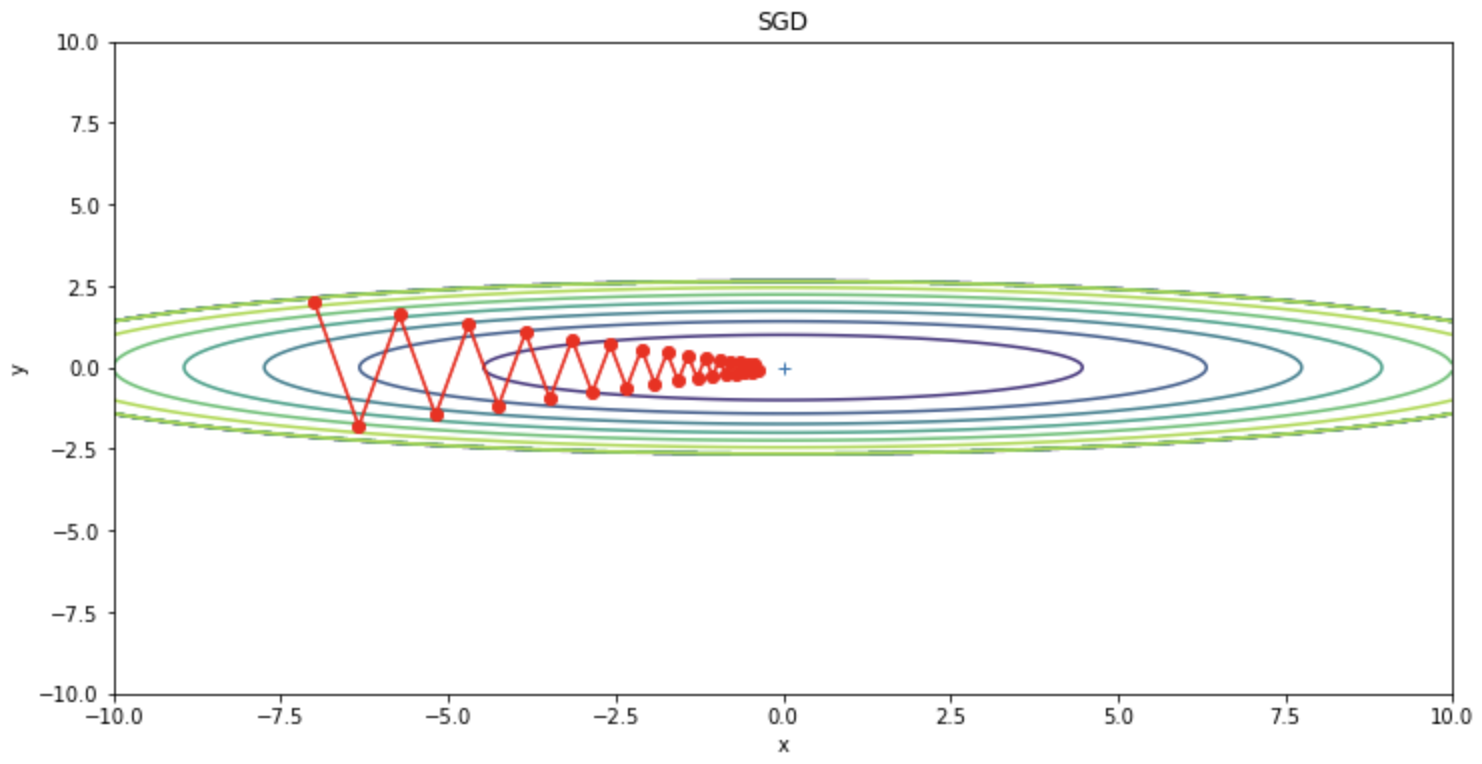
SGD dapat dilihat berosilasi secara zigzag. Osilasi ini merupakan jalur yang tidak efisien dan merupakan faktor yang memperlambat pembelajaran. Dengan demikian, jika bentuk fungsi tidak isotropik, SGD akan berosilasi zig-zag dan mencari pada jalur yang tidak efisien.

Untuk menekan osilasi ini, Momentum, AdaGrad, dan RMSProp, modifikasi AdaGrad, diturunkan; Momentum dari perspektif turunan, dan AdaGrad dan RMSProp dari perspektif tingkat pembelajaran, menggunakan perubahan gradien masa lalu untuk menekan osilasi SDG.

Momentum

Momentum adalah algoritma yang menambahkan momentum (istilah inersia) ke SGD. Momentum adalah rata-rata bergerak dari gradien. Momentum diwakili oleh persamaan pembaruan berikut.

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
            params[key] += self.v[key]

optimizer = Momentum(lr=0.1)

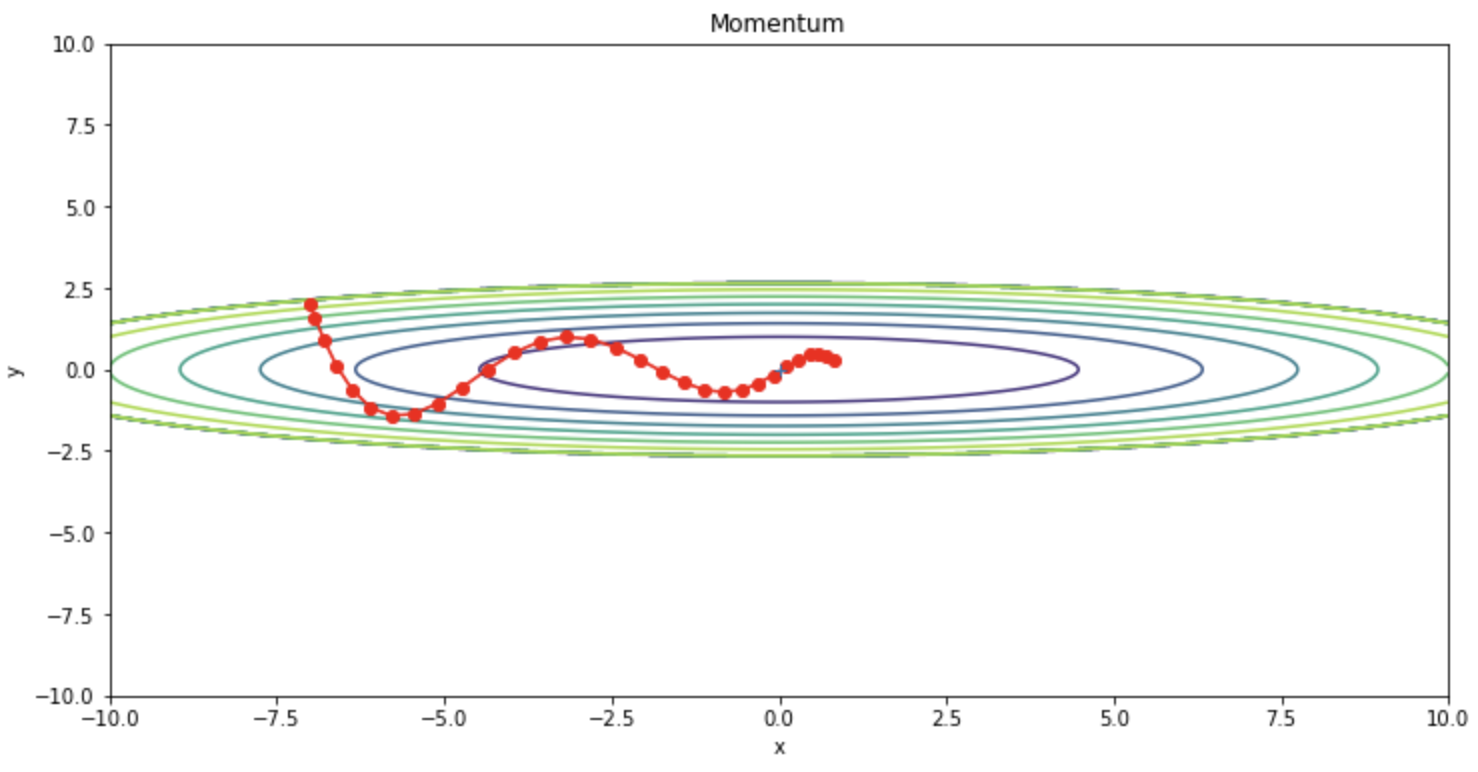
SMomentum

Kita dapat mengonfirmasi bahwa osilasi berkurang dibandingkan dengan SGD.

AdaGrad

AdaGrad menekan osilasi SGD dengan menyesuaikan laju pembelajaran. Berikut ini adalah rumus pembaruan untuk AdaGrad.

v_{t+1} = v_t + (\frac{\partial L}{\partial w_t})^2

w_{t+1} = w_t - \frac{\eta}{\sqrt{v_{t+1}}}\frac{\partial L}{\partial w_t}

$v_{t+1}$ adalah kuadrat dari gradien $\frac{\partial L}{\partial w_t}$ , yang menjadi lebih besar ketika perubahan gradien besar. Juga, karena $(\frac{\partial L}{\partial w_t})^2$ selalu positif, $v_{t+1}$ meningkat dengan setiap pembaruan. Oleh karena itu, tingkat pembelajaran $\frac{\eta}{\sqrt{v_{t+1}}}$ $ dari jumlah pembaruan $w_{t+1}$ menjadi lebih kecil ketika berosilasi dan juga menjadi lebih kecil dengan setiap pembaruan. Hal ini memungkinkan untuk mencari area yang luas pada awalnya dan kemudian secara bertahap mempersempit area pencarian untuk pencarian yang lebih efisien.

Kode implementasi AdaGrad ditunjukkan di bawah ini.

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

optimizer = AdaGrad(lr=1.5)

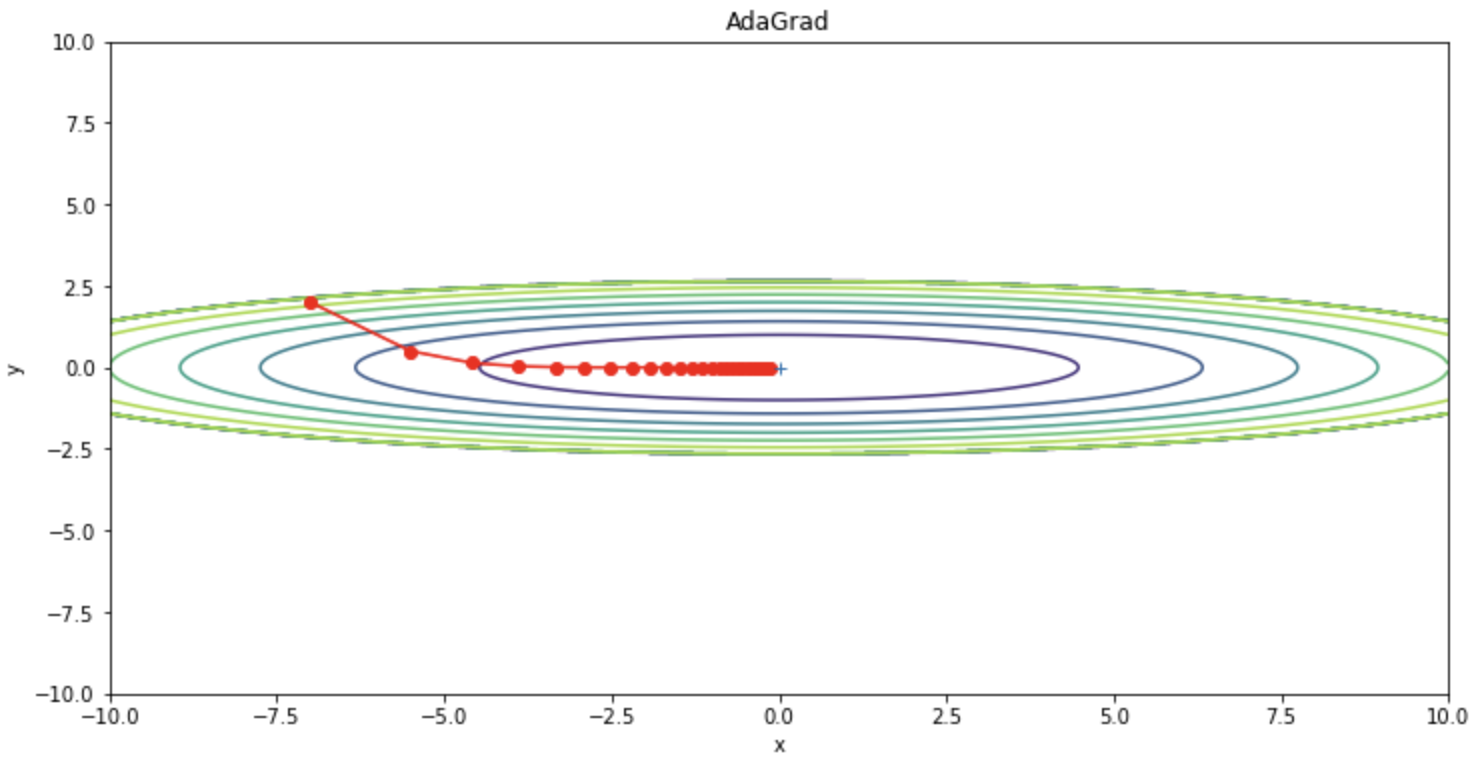
AdaGrad

Dapat dilihat bahwa osilasi berkurang dibandingkan dengan SGD.

Di sisi lain, AdaGrad memiliki kelemahan yaitu jumlah update yang terus menurun, sehingga jumlah update bisa menjadi hampir nol di tengah-tengah proses, menyebabkan optimasi berhenti. Dengan kata lain, jika pelatihan dilakukan tanpa batas waktu, jumlah update akan mencapai nol dan tidak ada update yang akan dilakukan sama sekali. Untuk mengatasi masalah ini, metode RMSProp diciptakan.

RMSProp

RMSProp memperbaiki masalah pembelajaran AdaGrad yang lambat karena tingkat pembaruan yang rendah.

v_{t+1} = \rho v_t + (1- \rho) (\frac{\partial L}{\partial w_t})^2

w_{t+1} = w_t - \frac{\eta}{\sqrt{v_{t+1}}}\frac{\partial L}{\partial w_t}

$\rho$ mengurangi tingkat pembelajaran sehingga informasi gradien yang lebih baru tercermin, daripada secara seragam mencerminkan semua gradien masa lalu.

Adam

Adam (ADaptive Moment Estimation) adalah perpaduan Momentum dan RMSProps dan merupakan algoritma optimasi yang banyak digunakan yang sering mengungguli algoritma optimasi lainnya. Bobot-bobot diperbaharui seperti pada rumus pembaharuan berikut ini.

v_{t+1} = \beta v_t + (1- \beta)\frac{\partial L}{\partial w_t}

s_{t+1} = \rho v_t + (1- \rho) (\frac{\partial L}{\partial w_t})^2

w_{t+1} = w_t - \eta \frac{v_{t+1}}{\sqrt{s_{t+1}}}

Kode implementasi Adam ditunjukkan di bawah ini.

class Adam:
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

optimizer = Adam(lr=0.3)

Adam

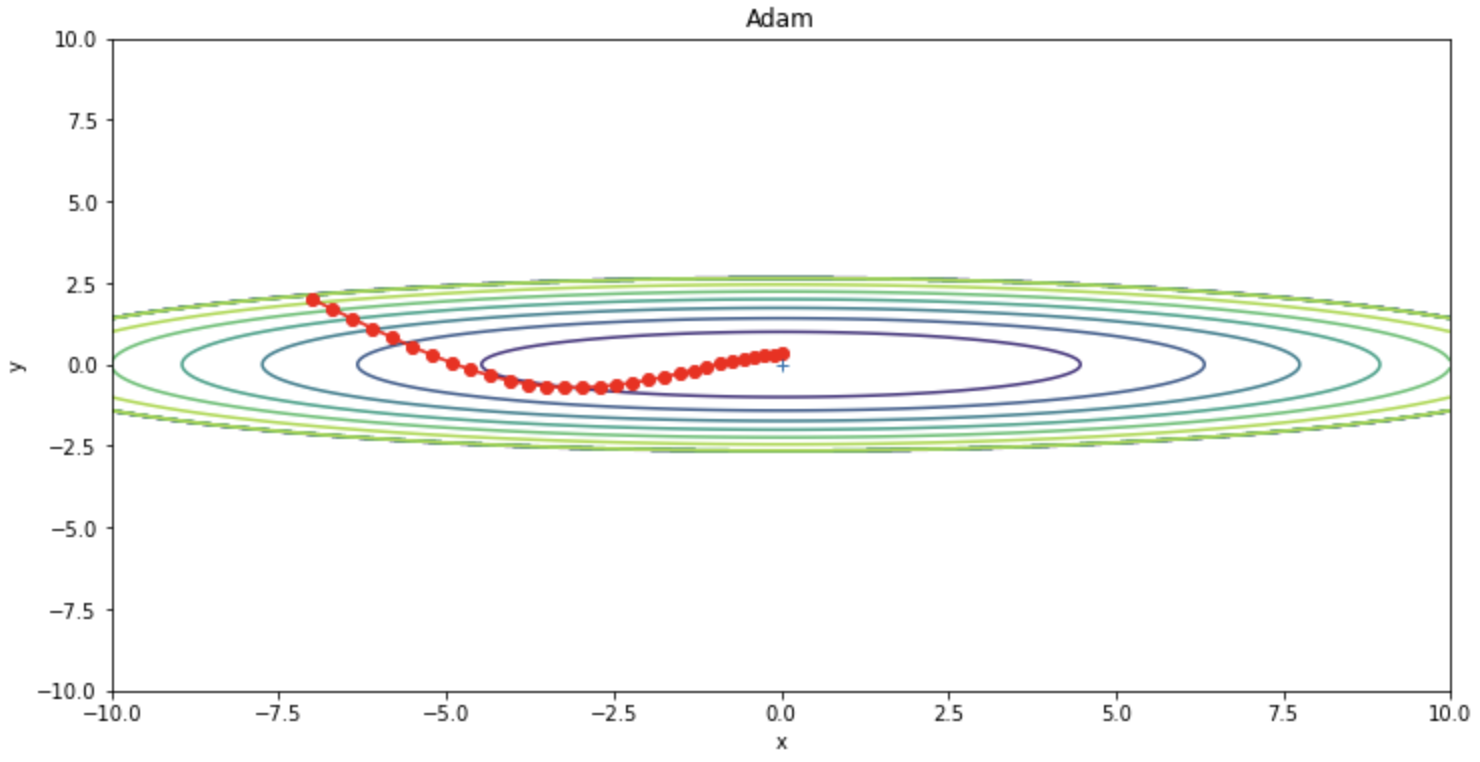
Ringkasan kode

Berikut ini adalah ringkasan kode yang digunakan dalam proyek ini.

import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

class SGD:
    """SGD"""
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

class Momentum:
    """Momentum SGD"""
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
            params[key] += self.v[key]

class AdaGrad:
    """AdaGrad"""
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

class RMSprop:
    """RMSprop"""
    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):
    return x / 10.0, 2.0*y

init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0


optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
# optimizers["RMSprop"] = RMSprop(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)


    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)

    # for simple contour line
    mask = Z > 7
    Z[mask] = 0

    # plot
    plt.figure(figsize=(12,6))
    # plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")

plt.show()