Pendahuluan

Distribusi aktivasi pada lapisan tersembunyi memainkan peran penting dalam proses pembelajaran jaringan saraf. Aktivasi yang terdistribusi dengan baik memungkinkan jaringan belajar fungsi yang lebih kompleks dan generalisasi lebih baik terhadap data baru yang tidak terlihat sebelumnya. Dengan menganalisis distribusi aktivasi dalam lapisan tersembunyi, peneliti dan praktisi dapat mendiagnosis masalah potensial, mengoptimalkan performa, dan meningkatkan efisiensi keseluruhan model.

Metode untuk Menganalisis Distribusi Aktivasi

Untuk memahami distribusi aktivasi pada lapisan tersembunyi dengan lebih baik, berbagai teknik visualisasi dan analisis dapat diterapkan:

• Histogram
  Histogram adalah metode umum untuk memvisualisasikan distribusi aktivasi. Dengan memplot frekuensi aktivasi dalam rentang nilai tertentu, histogram memberikan wawasan tentang bentuk dan penyebaran distribusi, yang dapat membantu mengidentifikasi masalah seperti gradien yang menghilang atau meledak.

• Density Plot
  Density plot menyediakan representasi yang halus dan kontinu dari distribusi aktivasi. Hal ini dapat membantu mengungkap struktur distribusi yang mendasar dan mengidentifikasi area potensial yang perlu diperhatikan, seperti neuron mati atau kurangnya keragaman nilai aktivasi.

• Cumulative Distribution Function (CDF) Plot
  CDF plot memvisualisasikan probabilitas kumulatif dari nilai aktivasi. Dengan menganalisis kemiringan plot CDF, kita dapat mengidentifikasi wilayah di mana aktivasi terkonsentrasi atau jarang, yang dapat memberikan strategi untuk meningkatkan distribusi.

Masalah Distribusi Aktivasi Umum

Beberapa masalah dalam distribusi aktivasi dapat berdampak negatif pada proses pembelajaran jaringan saraf:

• Gradien Menghilang
  Gradien yang menghilang adalah masalah di mana nilai gradien menjadi terlalu kecil, menyebabkan bobot jaringan diperbarui sangat lambat atau tidak sama sekali. Masalah ini dapat menyebabkan performa yang buruk dan konvergensi yang lambat. Hal ini sering terjadi ketika menggunakan fungsi aktivasi dengan rentang nilai output yang terbatas, seperti fungsi sigmoid atau tangen hiperbolik.

• Gradien Meledak
  Gradien yang meledak terjadi ketika nilai gradien menjadi terlalu besar, menyebabkan ketidakstabilan dalam proses pembelajaran dan berpotensi menyebabkan model menyebar. Masalah ini lebih umum terjadi pada jaringan yang lebih dalam dan dapat dimitigasi dengan menggunakan teknik inisialisasi bobot yang tepat, gradient clipping, atau teknik normalisasi.

• Neuron Mati
  Neuron mati merujuk pada situasi di mana beberapa neuron dalam lapisan tersembunyi secara konsisten mengeluarkan nilai yang sama, terlepas dari input. Hal ini dapat terjadi ketika menggunakan fungsi aktivasi yang memiliki daerah gradien nol, seperti fungsi ReLU. Neuron mati dapat menghambat proses pembelajaran, karena mereka tidak memberikan kontribusi yang bermakna pada output jaringan.

Mengoptimalkan Distribusi Aktivasi

Untuk mengatasi masalah yang disebutkan di atas dan mengoptimalkan distribusi aktivasi pada lapisan tersembunyi, beberapa teknik dapat diterapkan:

• Memilih Fungsi Aktivasi yang Tepat
  Menggunakan fungsi aktivasi yang memungkinkan rentang nilai output dan gradien yang lebih luas dapat membantu mencegah gradien yang menghilang atau meledak. Misalnya, ReLU dan varian-varian nya telah menjadi populer karena kemampuan mereka untuk mempertahankan gradien non-nol pada rentang input yang besar.

• Adaptive Learning Rates
  Menggunakan algoritma adaptive learning rate, seperti Adam atau RMSProp, dapat membantu mengurangi efek gradien yang menghilang atau meledak dengan menyesuaikan learning rate untuk setiap bobot secara individual.

• Teknik Inisialisasi Bobot
  Inisialisasi bobot yang tepat, seperti inisialisasi Xavier atau He, dapat membantu mencegah gradien yang menghilang atau meledak dengan memastikan bahwa bobot awal tidak menyebabkan aktivasi menjadi terlalu kecil atau terlalu besar.

• Teknik Regularisasi
  Mengaplikasikan teknik regularisasi, seperti L1 atau L2 regularization, dapat membantu mengurangi efek neuron mati dengan mendorong kejarangan atau mencegah bobot dari menjadi terlalu besar.

• Teknik Normalisasi
  Teknik normalisasi, seperti batch normalization atau layer normalization, dapat membantu menstabilkan proses pembelajaran dan meningkatkan distribusi aktivasi dengan menormalisasi input ke setiap lapisan tersembunyi selama pelatihan. Hal ini dapat menyebabkan konvergensi yang lebih cepat dan generalisasi yang lebih baik.

• Gradient Clipping
  Gradient clipping adalah teknik yang membatasi magnitudo gradien selama backpropagation. Dengan mencegah gradien menjadi terlalu besar, dapat membantu mengurangi efek gradien yang meledak dan meningkatkan stabilitas proses pembelajaran.

• Skip Connection
  Skip connection, seperti yang digunakan dalam arsitektur Residual Networks (ResNet), memungkinkan gradien mengalir lebih mudah melalui jaringan dengan melewati beberapa lapisan. Hal ini dapat membantu mengatasi masalah gradien yang menghilang, terutama pada jaringan yang lebih dalam.

Teknik untuk Distribusi Aktivasi yang Lebih Baik

Dalam bab ini, saya akan membahas berbagai teknik yang dapat diterapkan untuk meningkatkan distribusi aktivasi pada lapisan tersembunyi, sehingga meningkatkan performa dan efisiensi jaringan saraf.

Inisialisasi Bobot

Inisialisasi bobot dalam jaringan saraf memiliki dampak yang signifikan pada distribusi aktivasi. Inisialisasi bobot yang tepat dapat mencegah gradien yang menghilang atau meledak dan mempromosikan konvergensi yang lebih cepat. Beberapa metode inisialisasi bobot yang populer adalah:

• Inisialisasi Xavier (Glorot)
  Metode ini mengatur bobot awal berdasarkan ukuran unit input dan output pada lapisan. Metode ini sangat efektif ketika digunakan dengan fungsi aktivasi sigmoid atau tangen hiperbolik.

• Inisialisasi He
  Serupa dengan inisialisasi Xavier, inisialisasi He juga mempertimbangkan ukuran unit input dan output, tetapi dirancang khusus untuk ReLU dan varian-varian nya.

• Inisialisasi LeCun
  Metode ini dirancang khusus untuk fungsi aktivasi sigmoid dan tangen hiperbolik dan hanya mempertimbangkan ukuran unit input pada lapisan.

Normalisasi Batch

Normalisasi batch adalah teknik yang mengnormalisasi input ke setiap lapisan tersembunyi selama pelatihan dengan menskalakan dan menggeser aktivasi. Ini membantu menstabilkan proses pembelajaran, mempercepat konvergensi, dan meningkatkan performa generalisasi jaringan. Normalisasi batch dapat sangat berguna dalam menangani masalah gradien yang menghilang atau meledak dan mempromosikan aktivasi yang terdistribusi lebih merata.

Normalisasi Lapisan

Normalisasi lapisan adalah alternatif untuk normalisasi batch, khususnya berguna ketika menangani urutan yang panjang atau ukuran batch yang kecil. Alih-alih mengnormalisasi input di seluruh batch, normalisasi lapisan mengnormalisasi input di seluruh fitur dalam setiap lapisan tersembunyi. Ini dapat menyebabkan distribusi aktivasi yang lebih stabil dan dinamika pembelajaran yang lebih baik.

Regularisasi

Teknik regularisasi dapat membantu meningkatkan distribusi aktivasi dengan mendorong kejarangan atau mencegah bobot dari menjadi terlalu besar. Beberapa metode regularisasi yang umum adalah:

• Regularisasi L1
  Regularisasi L1 menambahkan pengali L1, sebanding dengan nilai absolut dari bobot, ke fungsi kerugian. Hal ini mendorong kejarangan dalam matriks bobot, yang dapat membantu mengurangi efek neuron mati.

• Regularisasi L2
  Regularisasi L2 menambahkan pengali L2, sebanding dengan kuadrat dari bobot, ke fungsi kerugian. Hal ini mencegah bobot dari menjadi terlalu besar dan dapat membantu mengatasi masalah yang berkaitan dengan gradien yang menghilang atau meledak.

• Dropout
  Dropout adalah teknik regularisasi di mana sebagian acak dari neuron "didrop" atau dinonaktifkan sementara selama pelatihan. Hal ini mencegah model bergantung terlalu banyak pada setiap neuron dan mendorong aktivasi yang lebih merata.

Visualisasi Distribusi Aktivasi di Lapisan Tersembunyi

Pada bab ini, saya akan menunjukkan cara memvisualisasikan distribusi aktivasi di lapisan tersembunyi menggunakan kumpulan data Iris, yang merupakan kumpulan data publik yang berisi 150 sampel bunga iris. Kita akan melatih jaringan saraf feed-forward sederhana (FFNN) pada kumpulan data ini, menggambar histogram aktivasi.

Ikhtisar Dataset dan Model

Kumpulan data Iris terdiri dari 150 sampel, dengan 50 sampel dari masing-masing tiga spesies bunga iris (Iris setosa, Iris versicolor, dan Iris virginica). Setiap sampel memiliki empat fitur (panjang sepal, lebar sepal, panjang kelopak, dan lebar kelopak) dan label yang menunjukkan spesies.

Model FFNN kita akan memiliki arsitektur berikut:

1. Lapisan input dengan 4 simpul input.
2. Lapisan terhubung penuh (dense) dengan 64 unit dan aktivasi ReLU.
3. Lapisan terhubung penuh (dense) dengan 32 unit dan aktivasi ReLU.
4. Lapisan terhubung penuh (dense) dengan 16 unit dan aktivasi ReLU.
5. Lapisan output dengan 3 unit dan aktivasi softmax.

Pra-Pemrosesan dan Pelatihan

Kita akan memproses data dan melatih model menggunakan kode Python berikut dengan PyTorch:

import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import torch.nn.functional as F
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder

# Load and preprocess the data
iris = datasets.load_iris()
X = iris.data
y = iris.target

# Normalize the features
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# One-hot encode the target labels
encoder = OneHotEncoder()
y_onehot = encoder.fit_transform(y.reshape(-1, 1)).toarray()

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y_onehot, test_size=0.2, random_state=42)

# Convert the data to PyTorch tensors
X_train = Variable(torch.Tensor(X_train).float())
X_test = Variable(torch.Tensor(X_test).float())
y_train = Variable(torch.Tensor(y_train).float())
y_test = Variable(torch.Tensor(y_test).float())

# Define the model
class Iris_FFNN(nn.Module):
    def __init__(self):
        super(Iris_FFNN, self).__init__()
        self.fc1 = nn.Linear(4, 64)
        self.fc2 = nn.Linear(64, 32)
        self.fc3 = nn.Linear(32, 16)
        self.fc4 = nn.Linear(16, 3)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = F.relu(self.fc3(x))
        x = self.fc4(x)
        return x

model = Iris_FFNN()

# Set loss function and optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# Train the model
num_epochs = 500
for epoch in range(num_epochs):
    optimizer.zero_grad()
    outputs = model(X_train)
    loss = criterion(outputs, y_train)
    loss.backward()
    optimizer.step()
    if (epoch + 1) % 50 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item()}')

print('Finished training')

Visualisasi Distribusi Aktivasi

Untuk memvisualisasikan distribusi aktivasi di lapisan tersembunyi, kita akan menggambar histogram aktivasi untuk lapisan 1, 2, dan 3. Untuk melakukannya, kita akan membuat fungsi untuk mengekstrak aktivasi dari lapisan tersembunyi:

def get_activations(model, layer_indices, input_data):
    activations = []

    for index in layer_indices:
        activation_model = nn.Sequential(*(list(model.children())[:index+1]))
        activation = activation_model(input_data)
        activations.append(activation)

    return activations

Selanjutnya, kita akan memasukkan satu batch sampel pengujian melalui model yang telah dilatih dan mengumpulkan aktivasi dari lapisan tersembunyi:

# Get the activations from the hidden layers
hidden_layer_indices = [0, 1, 2]
activations = get_activations(model, hidden_layer_indices, X_test)

Sekarang, kita akan menggambar histogram aktivasi ini menggunakan Matplotlib:

import matplotlib.pyplot as plt

plt.style.use('ggplot')

def plot_activation_histograms(activations, layer_indices):
    num_layers = len(activations)

    fig, axes = plt.subplots(1, num_layers, figsize=(15, 5))

    for i, activation in enumerate(activations):
        layer_index = layer_indices[i]
        axes[i].hist(activation.detach().numpy().flatten(), bins=50, orientation='vertical', alpha=0.5)
        axes[i].set_title(f'Layer {layer_index + 1} Activations')
        axes[i].set_xlabel('Activation Value')

    axes[0].set_ylabel('Frequency')
    plt.tight_layout()
    plt.show()

plot_activation_histograms(activations, hidden_layer_indices)

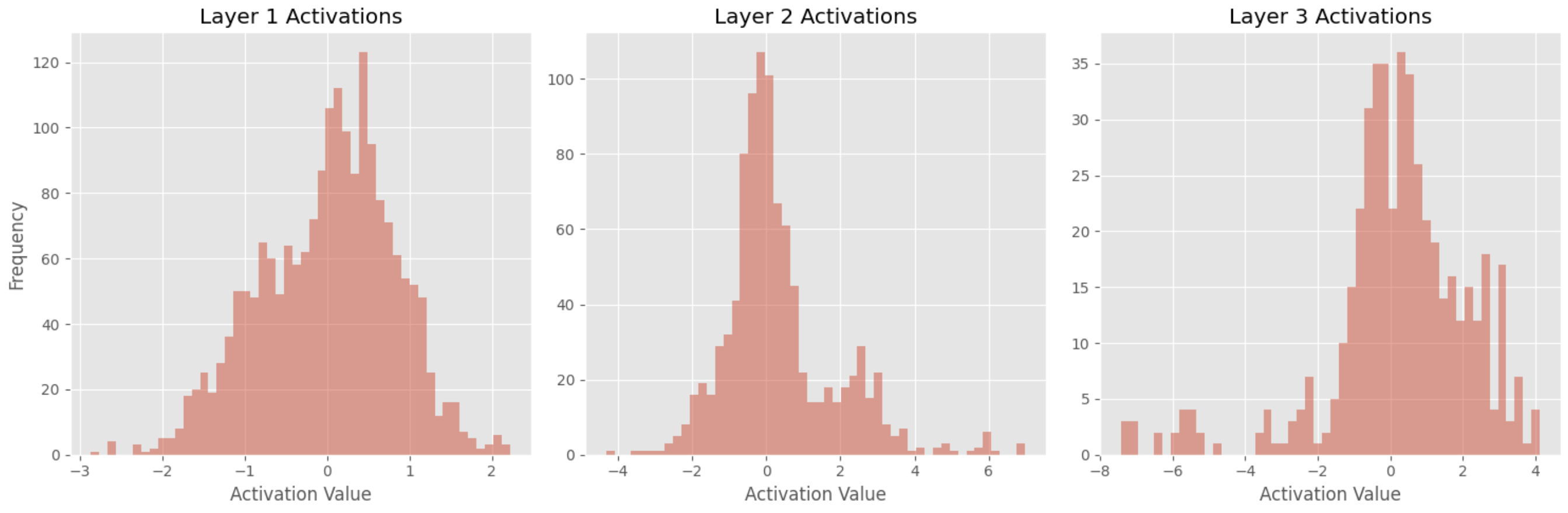
Interpretasi Hasil

Setelah menggambar histogram, kita dapat menganalisis distribusi aktivasi dan mengambil beberapa kesimpulan:

• Nilai paling sering adalah 0
  Fakta bahwa nilai aktivasi paling sering adalah 0 di seluruh 3 lapisan menunjukkan bahwa sebagian besar neuron dalam jaringan tidak diaktifkan oleh data masukan. Ini bisa jadi karena jaringan menggunakan fungsi aktivasi ReLU, yang mengeluarkan nilai 0 untuk semua nilai masukan negatif.

• Kurtosis Tertentu
  Peningkatan kurtosis dari lapisan 1 ke lapisan 3 menunjukkan bahwa distribusi nilai aktivasi menjadi lebih tajam dan memiliki ekor yang lebih berat ketika Anda bergerak lebih dalam ke dalam jaringan saraf. Ini bisa menunjukkan bahwa neuron di lapisan yang lebih dalam secara selektif merespons fitur-fitur tertentu dalam data masukan dan mengabaikan yang lain, yang bisa menjadi tanda jaringan belajar representasi yang lebih kompleks dari data.

• Rentang Lebih Luas
  Pelebaran rentang nilai aktivasi dari lapisan 1 ke lapisan 3 menunjukkan bahwa neuron di lapisan yang lebih dalam lebih sensitif terhadap variasi dalam data masukan. Ini bisa menjadi tanda jaringan belajar untuk mengekstrak fitur yang lebih halus dari data.