2023-04-07

Well Known Text (WKT)

What is Well Known Text (WKT)

Well Known Text (WKT) is a compact markup language designed to be readable by both machines and humans. It provides a means of representing geometric objects such as points, lines, and surfaces. The appeal of WKT lies in its ability to simplify the expression of geometric forms, making it an essential tool in various fields, including Geographic Information Systems (GIS), spatial databases, and computer graphics.

The text-based structure of WKT makes it inherently lightweight, yet comprehensive. It can articulate diverse shapes and forms, ranging from simple points to complex multi-dimensional geometric structures. This versatility provides a seamless way of translating mathematical representations of shapes into a format that can be effortlessly understood and manipulated.

Purpose and Functionality of WKT

The primary function of WKT is to standardize the representation of geometric entities, promoting interoperability across different software and systems dealing with spatial data. It is particularly instrumental in GIS and related applications where the storage, exchange, and processing of spatial information are of critical importance.

WKT not only supports a variety of geometry types, including simple shapes such as points, lines, and polygons, but it also accommodates more complex and composite structures, enabling robust and sophisticated geometrical analyses. Its structure also allows for the inclusion of additional dimensions, thereby facilitating the representation of 3D objects or those embedded with supplementary attributes.

Geometry Representation using WKT

WKT allows for a vast array of geometric entities to be represented, starting from the simplest objects to more complex structures.

Basic Geometry Types

WKT can represent basic geometrical entities that form the foundation for all complex structures.

Type	Figure	WKT
Point		`POINT (30 10)`
LineString		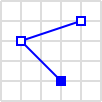`LINESTRING (30 10, 10 30, 40 40)`
Polygon		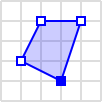`POLYGON ((30 10, 40 40, 20 40, 10 20, 30 10))`
Polygon		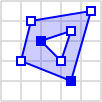`POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10), (20 30, 35 35, 30 20, 20 30))`

Point

A point represents a specific location within a space and is the most basic geometry type. In WKT, a point is written as POINT (30 10), where 30 and 10 are the X and Y coordinates, respectively.

LineString

A LineString, in simple terms, is a sequence of points that forms a line. A LineString in WKT may look like this: LINESTRING (30 10, 10 30, 40 40). This represents a line that moves from point (30,10) to point (10,30), and finally to point (40,40).

Polygon

A polygon is a shape defined by a series of points that form a closed loop. WKT represents polygons as POLYGON ((30 10, 40 40, 20 40, 10 20, 30 10)). Each pair of numbers denotes a point, and the series of points forms a polygon.

Advanced Geometry Types

WKT allows for a broader range of geometry types beyond the basic ones. These include advanced and composite structures, further expanding the possibilities of spatial representation:

POLYHEDRALSURFACE

A POLYHEDRALSURFACE is used to represent a three-dimensional object. It consists of multiple Polygon geometries which, together, form a three-dimensional shape.

POLYHEDRALSURFACE (
  ((40 40, 20 45, 45 30, 40 40)),
  ((20 35, 10 30, 10 10, 30 5, 45 20, 20 35)),
  ((30 20, 20 15, 20 25, 30 20))
)

TRIANGLE

A TRIANGLE is simply a polygon with three points. In WKT, you can represent it as follows:

TRIANGLE ((30 20, 40 40, 20 40, 30 20))

MULTIPOINT

MULTIPOINT is used to represent multiple discrete points. It is denoted as follows:

MULTIPOINT ((10 40), (40 30), (20 20), (30 10))

MULTILINESTRING

MULTILINESTRING represents multiple LineStrings. This is how you would denote it in WKT:

MULTILINESTRING ((10 10, 20 20, 10 40),
  (40 40, 30 30, 40 20, 30 10))

MULTIPOLYGON

MULTIPOLYGON is used when you want to represent multiple polygons. Here's how it can be represented:

MULTIPOLYGON (((30 20, 45 40, 10 40, 30 20)),
  ((15 5, 40 10, 10 20, 5 10, 15 5)))

TIN

A TIN (Triangulated Irregular Network) represents a network of triangles. A TIN is essentially a MultiPolygon with an added constraint - each polygon must be a triangle.

TIN (((0 0, 0 1, 1 0, 0 0)), ((0 0, 0 1, 1 1, 0 0)))

GEOMETRYCOLLECTION

A GEOMETRYCOLLECTION is used to represent a collection of any kind of geometry. It can contain Point, LineString, Polygon, and any of the other geometry types we have discussed.

GEOMETRYCOLLECTION (
  POINT (40 10),
  LINESTRING (10 10, 20 20, 10 40),
  POLYGON ((40 40, 20 45, 45 30, 40 40))
)

Dealing with Additional Dimensions in WKT

The essence of spatial data does not limit itself to just two dimensions. Real-world objects often exist in a three-dimensional space, and sometimes, additional dimensions are necessary to encapsulate attributes beyond the spatial. In this chapter, we explore how WKT accommodates these additional dimensions - the Z coordinate and M coordinate.

Z coordinate

The Z coordinate in WKT refers to the third spatial dimension, typically height or depth, allowing for the representation of three-dimensional objects. While WKT's visual depictions are inherently two-dimensional, adding a Z coordinate to the representation offers an additional layer of information about the geometric object. For instance, the Z value might represent elevation in a geographical context.

Here's how you would include the Z coordinate in a WKT POINT:

POINT Z (1 2 3)

In the example above, the point has an X coordinate of 1, a Y coordinate of 2, and a Z coordinate of 3.

M coordinate

Aside from spatial dimensions, WKT also supports the inclusion of a measure value, denoted as the M coordinate. This measure value is not spatial in nature, meaning it doesn't correspond to a physical dimension. Instead, it's often used to represent an attribute of the geometric object that is not tied to its spatial configuration.

For example, in a GIS application, the M value might represent time, making it possible to create 'space-time' trajectories. Alternatively, it might represent a property like temperature, rainfall, or population density at a particular point.

Here's how you would include the M coordinate in a WKT POINT:

POINT M (1 2 0)

In the example above, the point has an X coordinate of 1, a Y coordinate of 2, and a measure value of 0.

Combining Z and M Coordinates

There may be situations where it is useful to include both the Z and M coordinates for the same geometric object. WKT supports this with the ZM keyword: