2023-02-17

NLP 100 Exercise ch8：Neural Networks

Machine Learning

NLP

Introduction

The Tokyo Institute of Technology has created and maintains a collection of exercises on NLP called "NLP 100 Exercise".

https://nlp100.github.io/en/ch08.html

In this article, I will find sample answers to "Chapter 8: Neural Networks".

70. Generating Features through Word Vector Summation

Let us consider converting the dataset from the problem 50 to feature vectors. For example, we want to create a matrix $X$ (sequence of feature vectors of all instances) and a vector $Y$ (sequence of gold labels of all instances).

X = \begin{pmatrix} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \\ \dots \\ \boldsymbol{x}_n \\ \end{pmatrix} \in \mathbb{R}^{n \times d}, Y = \begin{pmatrix} y_1 \\ y_2 \\ \dots \\ y_n \\ \end{pmatrix} \in \mathbb{N}^{n}

Here, n represents a number of instances in training data. $\boldsymbol x_i \in \mathbb{R}^d$ and $y_i \in \mathbb N$ represent $i \in \{1, \dots, n\}$ -th feature vector and target (gold) label respectively. Note that the task is to classify a given headline into one of the following four categories: “Business”, “Science”, “Entertainment” and “Health”. Let us define that $\mathbb N_4$ represents a natural number smaller than 4 (including zero). Then a gold label of a given instance can be represented as $y_i \in \mathbb N_4$ . Let us also define that L represents the number of labels (This time L=4).

A feature vector of $i$ -th instance $x_i$ is computed as follows:

\boldsymbol x_i = \frac{1}{T_i} \sum_{t=1}^{T_i} \mathrm{emb}(w_{i,t})

where $i$ -th instance consists of $T_i$ tokens $(w_{i,1}, w_{i,2}, \dots, w_{i,T_i})$ and $\mathrm{emb}(w) \in \mathbb{R}^d$ represents a (size $d$ ) word vector corresponding word $w$ . In other words, $i$ -th article headline is represented as an average of word vectors of all words in the headline. For word embeddings, use pretrained word vector of dimension 300 (i.e., $d=300$ ).

A gold label of $i$ -th instance $y_i$ is defined as follows:

y_i = \begin{cases} 0 & (\textrm{if article }\boldsymbol x_i\textrm{ belong to Business category}) \\ 1 & (\textrm{if article }\boldsymbol x_i\textrm{ belong to Science category}) \\ 2 & (\textrm{if article }\boldsymbol x_i\textrm{ belong to Entertainment category}) \\ 3 & (\textrm{if article }\boldsymbol x_i\textrm{ belong to Health category}) \\ \end{cases}

Note that you do not have to strictly follow the definition above as long as there exist one-to-one mappings between the name of the category and the label index.

Based on the specifications above, create the following matrices and vectors and save them into binary files:

Training data feature matrix: $X_{\rm train} \in \mathbb{R}^{N_t \times d}$

Training data label matrix: $Y_{\rm train} \in \mathbb{N}^{N_t}$

Validation data feature matrix: $X_{\rm valid} \in \mathbb{R}^{N_v \times d}$

Validation data label matrix: $Y_{\rm valid} \in \mathbb{N}^{N_v}$

Test data feature matrix: $X_{\rm test} \in \mathbb{R}^{N_e \times d}$

Test data label matrix: $Y_{\rm test} \in \mathbb{N}^{N_e}$

Here, $N_t$ , $N_v$ , $N_e$ represent the number of instances in training data, validation data and test data, respectively.

!wget https://archive.ics.uci.edu/ml/machine-learning-databases/00359/NewsAggregatorDataset.zip
!unzip NewsAggregatorDataset.zip

import pandas as pd
from sklearn.model_selection import train_test_split
from gensim.models import KeyedVectors
import string
import torch

df = pd.read_csv('./newsCorporay.csv',
                 header=None,
                 sep='\t',
                 names=['ID', 'TITLE', 'URL', 'PUBLISHER', 'CATEGORY', 'STORY', 'HOSTNAME', 'TIMESTAMP']
                 )

df = df.loc[df['PUBLISHER'].isin(['Reuters', 'Huffington Post', 'Businessweek', 'Contactmusic.com', 'Daily Mail']), ['TITLE', 'CATEGORY']]

# split data
train, valid_test = train_test_split(
    df,
    test_size=0.2,
    shuffle=True,
    random_state=42,
    stratify=df['CATEGORY']
)
valid, test = train_test_split(
    valid_test,
    test_size=0.5,
    shuffle=True,
    random_state=42,
    stratify=valid_test['CATEGORY']
)

model = KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin.gz', binary=True)

def w2v(text):
  words = text.translate(str.maketrans(string.punctuation, ' '*len(string.punctuation))).split()
  vec = [model[word] for word in words if word in model]
  return torch.tensor(sum(vec) / len(vec))

# create x vectors
X_train = torch.stack([w2v(text) for text in train['TITLE']])
X_valid = torch.stack([w2v(text) for text in valid['TITLE']])
X_test = torch.stack([w2v(text) for text in test['TITLE']])

# create y vectors
category_dict = {'b': 0, 't': 1, 'e':2, 'm':3}
y_train = torch.tensor(train['CATEGORY'].map(lambda x: category_dict[x]).values)
y_valid = torch.tensor(valid['CATEGORY'].map(lambda x: category_dict[x]).values)
y_test = torch.tensor(test['CATEGORY'].map(lambda x: category_dict[x]).values)

# save
torch.save(X_train, 'X_train.pt')
torch.save(X_valid, 'X_valid.pt')
torch.save(X_test, 'X_test.pt')
torch.save(y_train, 'y_train.pt')
torch.save(y_valid, 'y_valid.pt')
torch.save(y_test, 'y_test.pt')

71. Building Single Layer Neural Network

Load matrices and vectors from the problem 70. Compute the following operations on training data:

\hat{y}_1=softmax(x_1W),\\\hat{Y}=softmax(X_{[1:4]}W)

Here, softmax refers to softmax function and $X_{[1:4]}∈\mathbb{R}^{4×d}$ is a vertical concatenation of $x_1$ , $x_2$ , $x_3$ , $x_4$ :

X_{[1:4]}=\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}

Matrix $W \in \mathbb{R}^{d \times L}$ is the weight of single-layer neural network. You may randomly initialize the weight for now (we will update the parameter in later questions). Note that $\hat{\boldsymbol y_1} \in \mathbb{R}^L$ represents a probability distribution over the category. Similarly, $\hat{Y} \in \mathbb{R}^{n \times L}$ represents a probability distribution of each instance in training data $x_1, x_2, x_3, x_4$ .

from torch import nn

class SimpleNet(nn.Module):
  def __init__(self, input_size, output_size):
    super().__init__()
    self.fc = nn.Linear(input_size, output_size, bias=False)
    nn.init.normal_(self.fc.weight, 0.0, 1.0)

  def forward(self, x):
    x = self.fc(x)
    return x

model = SimpleNet(300, 4)

y1_hat = torch.softmax(model(X_train[0]), dim=-1)
print(y1_hat)
print('\n')
Y_hat = torch.softmax(model.forward(X_train[:4]), dim=-1)
print(Y_hat)


>> tensor([0.6961, 0.0492, 0.0851, 0.1696], grad_fn=<SoftmaxBackward0>)
>>
>> tensor([[0.6961, 0.0492, 0.0851, 0.1696],
>>         [0.5393, 0.0273, 0.3510, 0.0824],
>>         [0.7999, 0.0519, 0.1301, 0.0182],
>>         [0.3292, 0.1503, 0.1286, 0.3919]], grad_fn=<SoftmaxBackward0>)

72. Calculating loss and gradients

Calculate the cross-entropy loss and the gradients for the matrix $W$ on a training sample $x_1$ and a set of samples $x_1$ , $x_2$ , $x_3$ , $x_4$ . The loss on a single sample is calculated using the following formula:

l_i=−log[\textrm{probability that sample } x_i \textrm{ is classified as } y_i]

The cross-entropy loss for a set of samples is the average of the losses of each sample included in the set.

criterion = nn.CrossEntropyLoss()

loss_1 = criterion(model(X_train[0]), y_train[0])
model.zero_grad()
loss_1.backward()
print(f'loss: {loss_1:.3f}')
print(f'gradient:\n{model.fc.weight.grad}')

loss = criterion(model(X_train[:4]), y_train[:4])
model.zero_grad()
loss.backward()
print(f'loss: {loss:.3f}')
print(f'gradient:\n{model.fc.weight.grad}')

>>loss: 2.074
>>gradient:
>>tensor([[ 0.0010,  0.0071,  0.0020,  ..., -0.0181,  0.0040,  0.0138],
>>        [ 0.0010,  0.0073,  0.0021,  ..., -0.0185,  0.0041,  0.0141],
>>        [-0.0075, -0.0549, -0.0157,  ...,  0.1400, -0.0308, -0.1068],
>>        [ 0.0055,  0.0406,  0.0116,  ..., -0.1034,  0.0228,  0.0789]])
>>
>>loss: 2.796
>>gradient:
>>tensor([[ 0.0241, -0.0344, -0.0255,  ..., -0.0221, -0.0253, -0.0218],
>>        [-0.0181,  0.0021,  0.0147,  ..., -0.0224, -0.0172,  0.0403],
>>        [-0.0018, -0.0030, -0.0008,  ...,  0.0443,  0.0063, -0.0327],
>>        [-0.0042,  0.0352,  0.0116,  ...,  0.0002,  0.0363,  0.0143]])

73. Learning with stochastic gradient descent

Update the matrix $W$ using stochastic gradient descent (SGD). The training should be terminated with an appropriate criterion, for example, “stop after 100 epochs”.

class Dataset(torch.utils.data.Dataset):
  def __init__(self, X, y):
    self.X = X
    self.y = y
    self.size = len(y)

  def __len__(self):
    return self.size

  def __getitem__(self, index):
    return [self.X[index], self.y[index]]

# create Dataset
train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)
test_ds = Dataset(X_test, y_test)

# create Dataloader
train_dl = torch.utils.data.DataLoader(train_ds,
                                       batch_size=1,
                                       shuffle=True
                                       )
valid_dl = torch.utils.data.DataLoader(valid_ds,
                                       batch_size=len(valid_ds),
                                       shuffle=False
                                       )
test_dl = torch.utils.data.DataLoader(test_ds,
                                      batch_size=len(test_ds),
                                      shuffle=False
                                      )

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
for epoch in range(num_epochs):
  model.train()
  loss_train = 0.0
  for i, (inputs, labels) in enumerate(train_dl):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()
    loss_train += loss.item()

  loss_train = loss_train / i
  model.eval()
  with torch.no_grad():
    inputs, labels = next(iter(valid_dl))
    outputs = model(inputs)
    loss_valid = criterion(outputs, labels)

  print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, loss_valid: {loss_valid:.3f}')

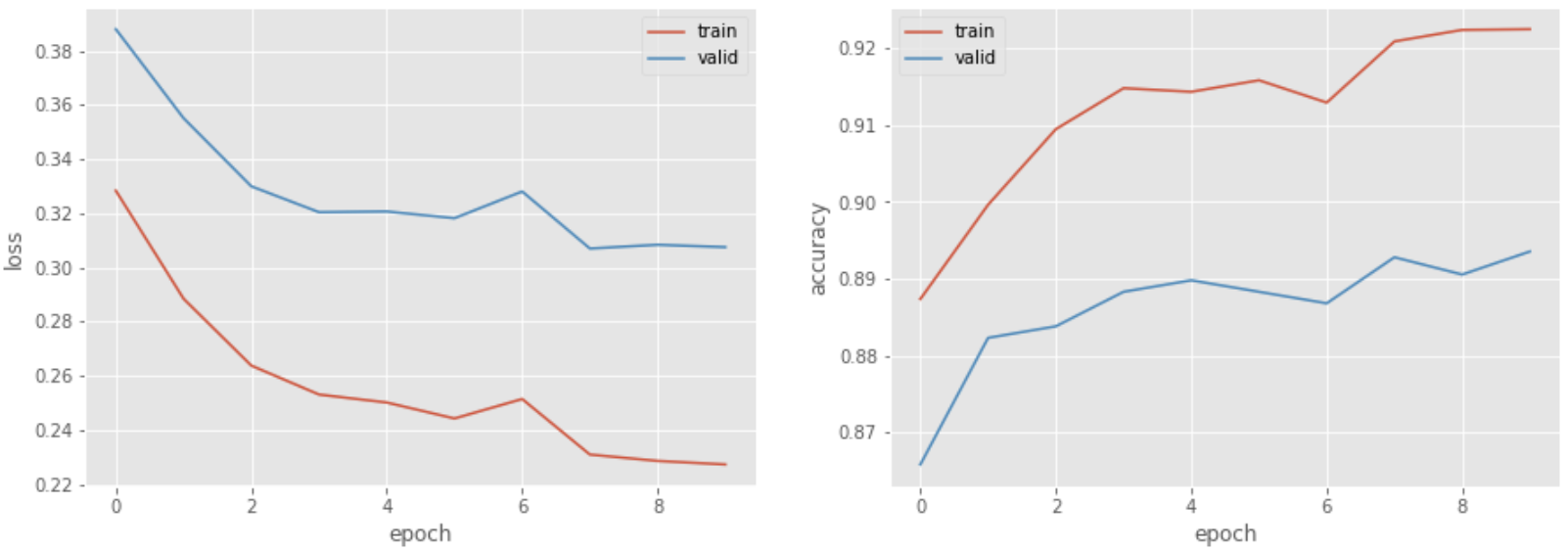
>> epoch: 1, loss_train: 0.471, loss_valid: 0.367
>> epoch: 2, loss_train: 0.309, loss_valid: 0.335
>> epoch: 3, loss_train: 0.281, loss_valid: 0.320
>> epoch: 4, loss_train: 0.265, loss_valid: 0.314
>> epoch: 5, loss_train: 0.256, loss_valid: 0.307
>> epoch: 6, loss_train: 0.250, loss_valid: 0.308
>> epoch: 7, loss_train: 0.244, loss_valid: 0.304
>> epoch: 8, loss_train: 0.240, loss_valid: 0.305
>> epoch: 9, loss_train: 0.237, loss_valid: 0.303
>> epoch: 10, loss_train: 0.234, loss_valid: 0.305

74. Measuring accuracy

Find the classification accuracy over both the training and evaluation data using the matrix obtained in the problem 73.

def calc_accuracy(model, loader):
  model.eval()
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      outputs = model(inputs)
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()
  return correct / total

acc_train = calc_accuracy(model, train_dl)
acc_test = calc_accuracy(model, test_dl)
print(f'accuracy (train)：{acc_train:.3f}')
print(f'accuracy (test)：{acc_test:.3f}')

>> accuracy (train)：0.923
>> accuracy (test)：0.900

75. Plotting loss and accuracy

Modify the code from the problem 73 so that the loss and accuracy of both the training and the evaluation data are plotted on a graph after each epoch. Use this graph to monitor the progress of learning.

def calc_loss_and_accuracy(model, criterion, loader):
  model.eval()
  loss = 0.0
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      outputs = model(inputs)
      loss += criterion(outputs, labels).item()
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()
  return loss / len(loader), correct / total

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
log_train = []
log_valid = []
for epoch in range(num_epochs):
  model.train()
  for inputs, labels in train_dl:
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

  loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
  loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
  log_train.append([loss_train, acc_train])
  log_valid.append([loss_valid, acc_valid])

from matplotlib import pyplot as plt
import numpy as np

plt.style.use('ggplot')

fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log_train).T[0], label='train')
ax[0].plot(np.array(log_valid).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log_train).T[1], label='train')
ax[1].plot(np.array(log_valid).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()

76. Checkpoints

Modify the code from the problem 75 to write out checkpoints to a file after each epoch. Checkpoints should include values of the parameters such as weight matrices and the internal states of the optimization algorithm.

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
log_train = []
log_valid = []
for epoch in range(num_epochs):
  model.train()
  for inputs, labels in train_dl:
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

  loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
  loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
  log_train.append([loss_train, acc_train])
  log_valid.append([loss_valid, acc_valid])

  torch.save({
                'epoch': epoch,
                'model_state_dict': model.state_dict(),
                'optimizer_state_dict': optimizer.state_dict()
             },
             f'checkpoint_{epoch + 1}.pt'
             )

77. Mini-batches

Modify the code from the problem 76 to calculate the loss/gradient and update the values of matrix $W$ for every $B$ samples (mini-batch). Compare the time required for one learning epoch by changing the value of $B$ to $1,2,4,8,\dots$ .

import time

def train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, num_epochs):
  train_dl = torch.utils.data.DataLoader(train_ds, batch_size=batch_size, shuffle=True)
  valid_dl = torch.utils.data.DataLoader(valid_ds, batch_size=len(valid_ds), shuffle=False)

  log_train = []
  log_valid = []
  for epoch in range(num_epochs):
    s_time = time.time()
    model.train()
    for inputs, labels in train_dl:
      optimizer.zero_grad()
      outputs = model(inputs)
      loss = criterion(outputs, labels)
      loss.backward()
      optimizer.step()

    loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
    loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
    log_train.append([loss_train, acc_train])
    log_valid.append([loss_valid, acc_valid])

    torch.save({
        'epoch': epoch,
        'model_state_dict': model.state_dict(),
        'optimizer_state_dict': optimizer.state_dict()
        },
        f'checkpoint_{epoch + 1}.pt'
    )

    e_time = time.time()

    print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, accuracy_train: {acc_train:.3f}, loss_valid: {loss_valid:.3f}, accuracy_valid: {acc_valid:.3f}, {(e_time - s_time):.3f}sec')

  return {'train': log_train, 'valid': log_valid}

train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

for batch_size in [2 ** i for i in range(11)]:
  print(f'batch size: {batch_size}')
  log = train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, 1)

>> batch size: 1
>> epoch: 1, loss_train: 0.337, accuracy_train: 0.884, loss_valid: 0.385, accuracy_valid: 0.869, 3.993sec
>> batch size: 2
>> epoch: 1, loss_train: 0.303, accuracy_train: 0.896, loss_valid: 0.348, accuracy_valid: 0.879, 2.457sec
>> batch size: 4
>> epoch: 1, loss_train: 0.292, accuracy_train: 0.899, loss_valid: 0.341, accuracy_valid: 0.881, 1.220sec
>> batch size: 8
>> epoch: 1, loss_train: 0.288, accuracy_train: 0.901, loss_valid: 0.337, accuracy_valid: 0.887, 0.802sec
>> batch size: 16
>> epoch: 1, loss_train: 0.286, accuracy_train: 0.901, loss_valid: 0.336, accuracy_valid: 0.887, 0.592sec
>> batch size: 32
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.902, loss_valid: 0.334, accuracy_valid: 0.886, 0.396sec
>> batch size: 64
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.307sec
>> batch size: 128
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.246sec
>> batch size: 256
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.219sec
>> batch size: 512
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.195sec
>> batch size: 1024
>> epoch: 1, loss_train: 0.287, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.198sec

78. Training on a GPU

Modify the code from the problem 77 so that it runs on a GPU.

def calc_loss_and_accuracy(model, criterion, loader, device):
  model.eval()
  loss = 0.0
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      inputs = inputs.to(device)
      labels = labels.to(device)
      outputs = model(inputs)
      loss += criterion(outputs, labels).item()
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()

  return loss / len(loader), correct / total


def train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, num_epochs, device=None):
  model.to(device)

  train_dl = torch.utils.data.DataLoader(train_ds,
                                         batch_size=batch_size,
                                         shuffle=True)
  valid_dl = torch.utils.data.DataLoader(valid_ds,
                                         batch_size=len(valid_ds),
                                         shuffle=False)

  log_train = []
  log_valid = []
  for epoch in range(num_epochs):
    s_time = time.time()
    model.train()
    for inputs, labels in train_dl:
      optimizer.zero_grad()
      inputs = inputs.to(device)
      labels = labels.to(device)
      outputs = model.forward(inputs)
      loss = criterion(outputs, labels)
      loss.backward()
      optimizer.step()

    loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl, device)
    loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl, device)
    log_train.append([loss_train, acc_train])
    log_valid.append([loss_valid, acc_valid])

    torch.save({
        'epoch': epoch,
        'model_state_dict': model.state_dict(),
        'optimizer_state_dict': optimizer.state_dict()
        },
        f'checkpoint_{epoch + 1}.pt'
    )

    e_time = time.time()

    print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, accuracy_train: {acc_train:.3f}, loss_valid: {loss_valid:.3f}, accuracy_valid: {acc_valid:.3f}, {(e_time - s_time):.3f}sec')

  return {'train': log_train, 'valid': log_valid}

train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

device = torch.device('cuda')

for batch_size in [2 ** i for i in range(11)]:
  print(f'batch size: {batch_size}')
  log = train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, 1, device=device)

>> batch size: 1
>> epoch: 1, loss_train: 0.337, accuracy_train: 0.883, loss_valid: 0.392, accuracy_valid: 0.868, 13.139sec
>> batch size: 2
>> epoch: 1, loss_train: 0.300, accuracy_train: 0.898, loss_valid: 0.357, accuracy_valid: 0.882, 4.998sec
>> batch size: 4
>> epoch: 1, loss_train: 0.291, accuracy_train: 0.901, loss_valid: 0.349, accuracy_valid: 0.885, 2.623sec
>> batch size: 8
>> epoch: 1, loss_train: 0.287, accuracy_train: 0.901, loss_valid: 0.346, accuracy_valid: 0.882, 1.589sec
>> batch size: 16
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.902, loss_valid: 0.344, accuracy_valid: 0.886, 0.902sec
>> batch size: 32
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.544sec
>> batch size: 64
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.377sec
>> batch size: 128
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.292sec
>> batch size: 256
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.291sec
>> batch size: 512
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.145sec
>> batch size: 1024
>> epoch: 1, loss_train: 0.282, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.126sec

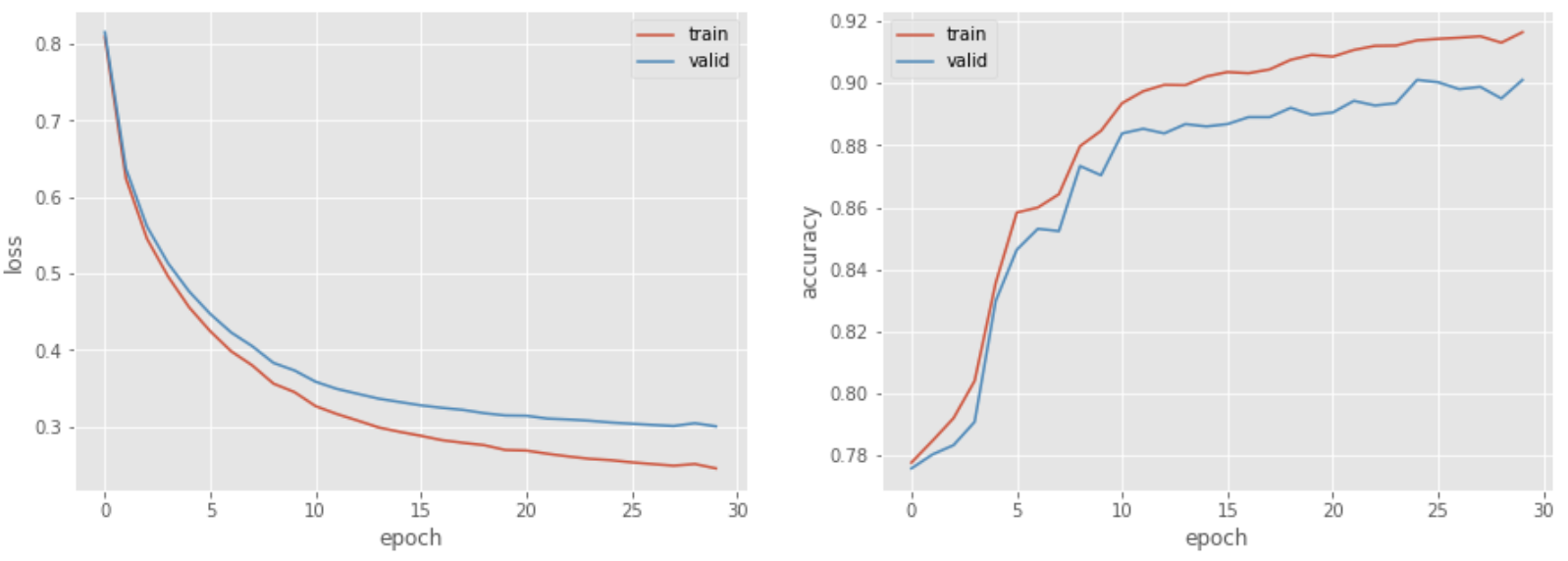
79. Multilayer Neural Networks

Modify the code from the problem 78 to create a high-performing classifier by changing the architecture of the neural network. Try introducing bias terms and multiple layers.

from torch.nn import functional as F

class MLPNet(nn.Module):
  def __init__(self, input_size, mid_size, output_size):
    super().__init__()
    self.fc1 = nn.Linear(input_size, mid_size)
    self.act = nn.ReLU()
    self.fc2 = nn.Linear(mid_size, output_size)
    self.dropout = nn.Dropout(0.2)
    nn.init.kaiming_normal_(self.fc1.weight)
    nn.init.kaiming_normal_(self.fc2.weight)

  def forward(self, x):
    x = self.fc1(x)
    x = self.act(x)
    x = self.dropout(x)
    x = self.fc2(x)
    return x

model = MLPNet(300, 128, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

device = torch.device('cuda')

log = train_model(train_ds, valid_ds, 128, model, criterion, optimizer, 30, device=device)

fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log['train']).T[0], label='train')
ax[0].plot(np.array(log['valid']).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log['train']).T[1], label='train')
ax[1].plot(np.array(log['valid']).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()

>> epoch: 1, loss_train: 0.809, accuracy_train: 0.778, loss_valid: 0.815, accuracy_valid: 0.776, 0.247sec
>> epoch: 2, loss_train: 0.624, accuracy_train: 0.785, loss_valid: 0.637, accuracy_valid: 0.780, 0.429sec
>> epoch: 3, loss_train: 0.545, accuracy_train: 0.792, loss_valid: 0.561, accuracy_valid: 0.783, 0.278sec
>> epoch: 4, loss_train: 0.496, accuracy_train: 0.804, loss_valid: 0.513, accuracy_valid: 0.791, 0.241sec
>> epoch: 5, loss_train: 0.456, accuracy_train: 0.836, loss_valid: 0.477, accuracy_valid: 0.830, 0.248sec
>> epoch: 6, loss_train: 0.425, accuracy_train: 0.858, loss_valid: 0.447, accuracy_valid: 0.846, 0.244sec
>> epoch: 7, loss_train: 0.398, accuracy_train: 0.860, loss_valid: 0.423, accuracy_valid: 0.853, 0.247sec
>> epoch: 8, loss_train: 0.380, accuracy_train: 0.864, loss_valid: 0.405, accuracy_valid: 0.852, 0.251sec
>> epoch: 9, loss_train: 0.356, accuracy_train: 0.880, loss_valid: 0.383, accuracy_valid: 0.873, 0.263sec
>> epoch: 10, loss_train: 0.345, accuracy_train: 0.885, loss_valid: 0.373, accuracy_valid: 0.870, 0.260sec
>> epoch: 11, loss_train: 0.327, accuracy_train: 0.894, loss_valid: 0.359, accuracy_valid: 0.884, 0.243sec
>> epoch: 12, loss_train: 0.317, accuracy_train: 0.897, loss_valid: 0.349, accuracy_valid: 0.885, 0.246sec
>> epoch: 13, loss_train: 0.308, accuracy_train: 0.899, loss_valid: 0.343, accuracy_valid: 0.884, 0.260sec
>> epoch: 14, loss_train: 0.299, accuracy_train: 0.899, loss_valid: 0.336, accuracy_valid: 0.887, 0.241sec
>> epoch: 15, loss_train: 0.293, accuracy_train: 0.902, loss_valid: 0.332, accuracy_valid: 0.886, 0.237sec
>> epoch: 16, loss_train: 0.288, accuracy_train: 0.904, loss_valid: 0.328, accuracy_valid: 0.887, 0.247sec
>> epoch: 17, loss_train: 0.282, accuracy_train: 0.903, loss_valid: 0.325, accuracy_valid: 0.889, 0.239sec
>> epoch: 18, loss_train: 0.279, accuracy_train: 0.904, loss_valid: 0.322, accuracy_valid: 0.889, 0.252sec
>> epoch: 19, loss_train: 0.276, accuracy_train: 0.908, loss_valid: 0.318, accuracy_valid: 0.892, 0.241sec
>> epoch: 20, loss_train: 0.269, accuracy_train: 0.909, loss_valid: 0.315, accuracy_valid: 0.890, 0.241sec
>> epoch: 21, loss_train: 0.269, accuracy_train: 0.909, loss_valid: 0.314, accuracy_valid: 0.891, 0.240sec
>> epoch: 22, loss_train: 0.265, accuracy_train: 0.911, loss_valid: 0.311, accuracy_valid: 0.894, 0.251sec
>> epoch: 23, loss_train: 0.261, accuracy_train: 0.912, loss_valid: 0.309, accuracy_valid: 0.893, 0.243sec
>> epoch: 24, loss_train: 0.258, accuracy_train: 0.912, loss_valid: 0.308, accuracy_valid: 0.894, 0.237sec
>> epoch: 25, loss_train: 0.256, accuracy_train: 0.914, loss_valid: 0.305, accuracy_valid: 0.901, 0.240sec
>> epoch: 26, loss_train: 0.253, accuracy_train: 0.914, loss_valid: 0.304, accuracy_valid: 0.900, 0.244sec
>> epoch: 27, loss_train: 0.251, accuracy_train: 0.915, loss_valid: 0.302, accuracy_valid: 0.898, 0.236sec
>> epoch: 28, loss_train: 0.249, accuracy_train: 0.915, loss_valid: 0.301, accuracy_valid: 0.899, 0.239sec
>> epoch: 29, loss_train: 0.251, accuracy_train: 0.913, loss_valid: 0.304, accuracy_valid: 0.895, 0.241sec
>> epoch: 30, loss_train: 0.245, accuracy_train: 0.916, loss_valid: 0.300, accuracy_valid: 0.901, 0.241sec