What is the Chi-square distribution

The chi-square distribution is the probability distribution that the random variables X_1, X_2, \cdots, X_n follow when they are independent of each other and each follows a standard normal distribution N(0,1), where \chi^2 is

The probability density function of the chi-square distribution is expressed by the following equation:

The probability density function of the chi-square distribution, like the probability density function of the t-distribution, has only n parameters. The n are called degrees of freedom as in the t-distribution. The chi-square distribution is sometimes denoted as \chi^2(n).

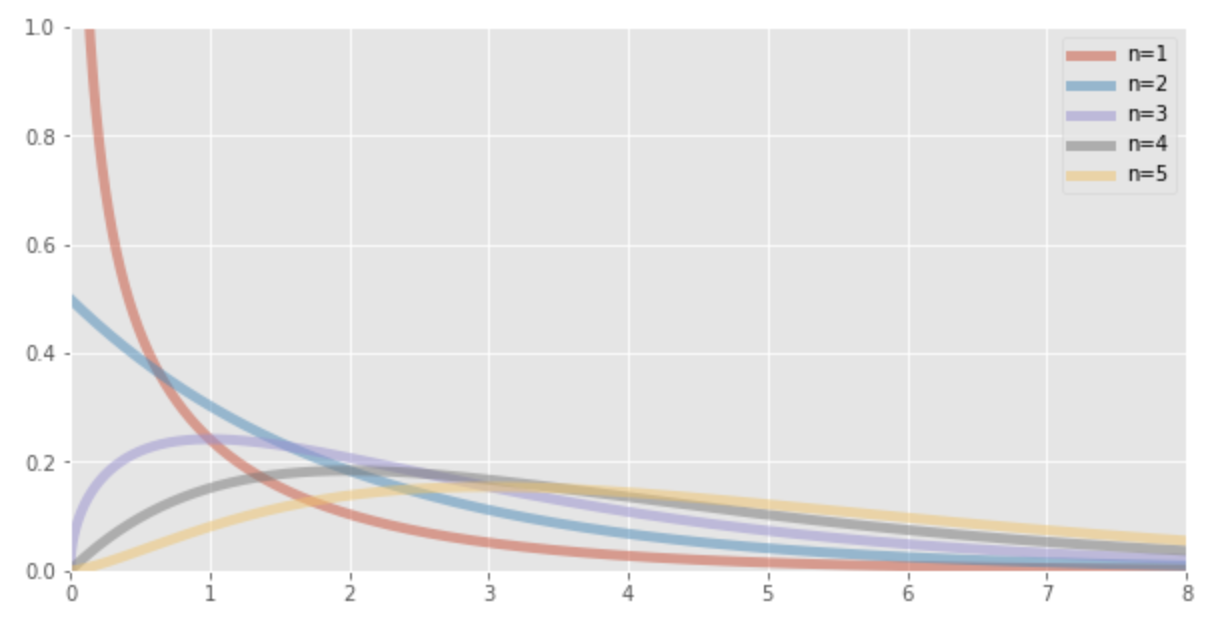
The graph of the chi-square distribution depends on the n degrees of freedom and looks like this.

Relationship to the standard normal distribution

The chi-square distribution with 1 degree of freedom is equal to the squared random variable X_1 following the standard normal distribution.

Expected value and variance of the chi-square distribution

The expected value and variance of the random variable X following the F distribution F(m, n) are respectively:

Chi-Square distribution table (upper side)

Since the chi-square distribution has only n parameters, the probabilities of the chi-square distribution can be summarized in a table called the chi-square distribution table. Below is a chi-square distribution table summarizing the degrees of freedom of the chi-square distribution with upper side probabilities \alpha equal to 0.1, 0.05, 0.025 and 0.01, respectively.

For example, if you want to find the upper 5% point of the chi-square distribution with 5 degrees of freedom, look for the value at the intersection of n=10 and \alpha=0.05. Thus, the upper 5th percentile point you are looking for is 11.07.

Reproductive property of chi-Square distribution

Suppose that the random variables X and Y follow the chi-square distribution respectively and are independent of each other as follows:

In this case, X + Y follows the following chi-square distribution:

This property is called the reproductive property.

Random sample from a population following a normal distribution and chi-square distribution

In a randomly selected samples X_1, X_2, \cdots, X_n from a population following a normal distribution of N(\mu,\sigma^2), where each X follows a normal distribution independently of each other, the following random variable W follows a chi-square distribution with n-1 degrees of freedom.

Also, as the unbiased variance is S^2, W can also be expressed as follows:

Python Code

The following is the Python code used to draw the chi-square distribution.

from scipy.stats import chi2
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

x = np.linspace(0, 8, 10000)

k_deg = [1, 2, 3, 4, 5] # degree of freedom

for i in k_deg:
    plt.plot(x, chi2.pdf(x, i), linestyle='-', label='n={}'.format(i), lw=5, alpha=0.5)

plt.xlim(0, 8)
plt.ylim(0, 1)
plt.legend()
plt.show()