What is an activation function?

An activation function in neural networks is a function that converts an input value into another value for output from one neuron to the next. The integrated value, which is the sum of the input to the neuron and the weight product plus the bias, is converted into a signal that represents the neuron's excited state. Without the activation function, the operation of a neuron would simply be a sum of products, and the expressive power of the neural network would be lost.

There are various types of activation functions. In this article, I will introduce typical activation functions.

Step function

Step function is a staircase function. It is represented by the following equation.

The step function, when executed in Python, looks like the following code

import numpy as np
import matplotlib.pyplot as plt

def step_function(x):
    return np.where(x<=0, 0, 1)

x = np.linspace(-5, 5)
y = step_function(x)

plt.plot(x, y)
plt.show()

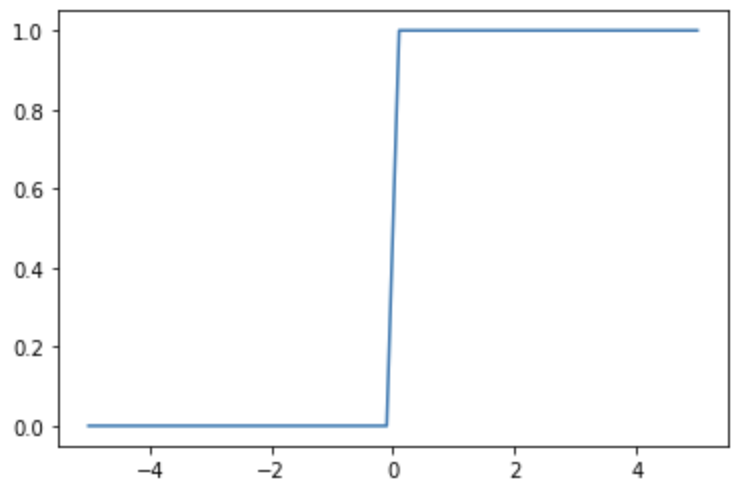
While the step function can simply represent the excited state of a neuron as 0 or 1, it has the disadvantage of not being able to represent states between 0 and 1.

Sigmoid function

A sigmoid function is a function that varies smoothly between 0 and 1. It is represented by the following equation

The sigmoid function, when executed in Python, looks like the following code.

import numpy as np
import matplotlib.pylab as plt

def sigmoid_function(x):
    return 1/(1+np.exp(-x))

x = np.linspace(-5, 5)
y = sigmoid_function(x)

plt.plot(x, y)
plt.show()

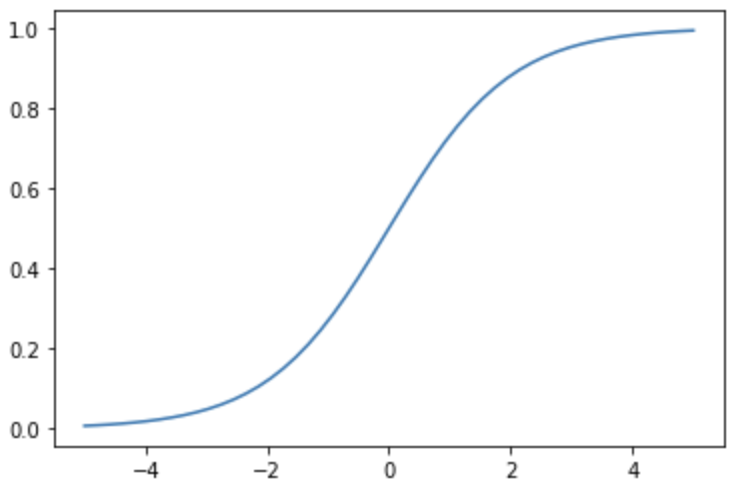
Sigmoid functions are smoother than step functions and can express intermediate between 0 and 1. In addition, sigmoid functions are characterized by their easy-to-handle derivatives.

tanh function

The tanh function is a function that varies smoothly between -1 and 1. The shape of the curve is similar to that of the sigmoid function, but the tanh function is symmetric about 0.

The tanh function, when executed in Python, looks like the following code

import numpy as np
import matplotlib.pylab as plt

x = np.linspace(-5, 5)
y = np.tanh(x

plt.plot(x, y)
plt.show()

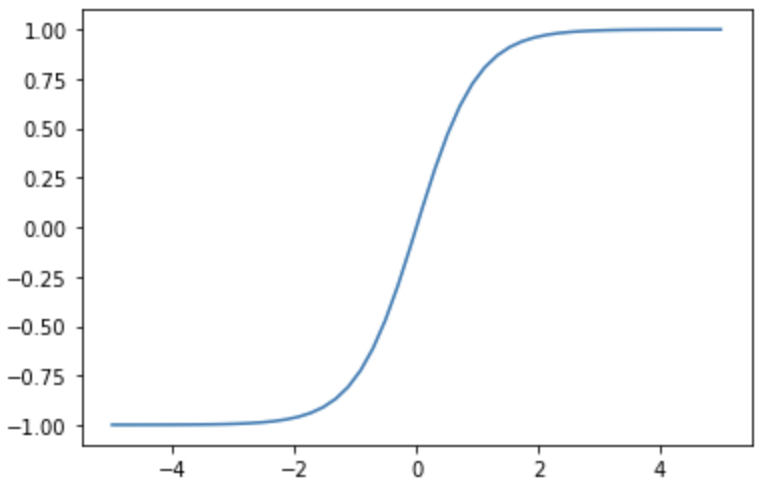
ReLU function

The ReLU function is a function whose output y is 0 if the input x is negative and y is x if x is positive. The ReLU function is represented by the following equation.

The ReLU function, when executed in Python, looks like the following code

import numpy as np
import matplotlib.pylab as plt

x = np.linspace(-5, 5)
y = np.where(x <= 0, 0, x)

plt.plot(x, y)
plt.show()

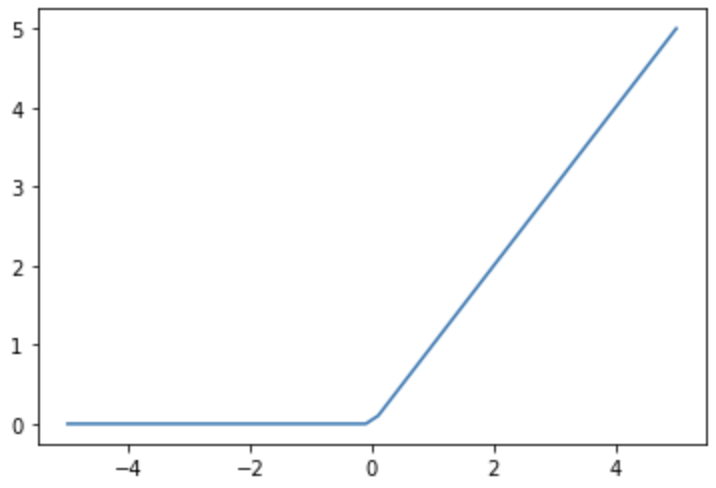
The ReLU function is often used as an activation function other than the output layer because of its simplicity and stable training even when the number of layers increases.

Identity function

An identity function is a function that returns the input as it is as an output. It is represented by the following equation.

The Python code for the identity function is as follows

import numpy as np
import matplotlib.pylab as plt

x = np.linspace(-5, 5)
y = x

plt.plot(x, y)
plt.show()

Identity functions are often used in regression problems because the range of output is unlimited and continuous, making them suitable for predicting continuous numbers.

Softmax function

The softmax function is an activation function suitable for classification problems. If the output of the activation function is y, the input is x, and the number of neurons in the same layer is n, the softmax function is represented by the following equation.

It also has the following properties of softmax functions.

• The sum of the outputs of the same layer sums to 1
• Values of 0<y<1 are output

Because of these properties, softmax functions are used as output layers for multiclass classification.

The softmax function can be implemented with the following code

import numpy as np

def softmax_function(x):
    return np.exp(x)/np.sum(np.exp(x))

y = softmax_function(np.array([1,2,3]))
print(y)

[0.09003057 0.24472847 0.66524096]