Apa itu Z-Score

Z-Score, juga dikenal sebagai skor standar, adalah ukuran seberapa banyak suatu titik data atau pengamatan individu dari rerata distribusi dalam satuan standar deviasi. Konsep ini sering digunakan dalam statistik deskriptif untuk memungkinkan perbandingan titik data dari berbagai dataset atau distribusi. Secara keseluruhan, z-score membantu dalam standarisasi dan normalisasi data.

Rumus untuk menghitung z-score adalah sebagai berikut:

di mana:

• Z = z-score
• X = titik data individu atau pengamatan
• \mu = rerata distribusi
• \sigma = standar deviasi distribusi

Pentingnya dan Aplikasi Z-Score

Z-Score memainkan peran penting dalam memahami dan menafsirkan data dalam berbagai bidang seperti pendidikan, keuangan, olahraga, dan kesehatan. Dengan standarisasi data, z-score memungkinkan perbandingan titik data antar populasi atau pengukuran yang berbeda, sehingga memungkinkan untuk mengidentifikasi outlier, mengevaluasi kinerja, dan menilai posisi relatif suatu pengamatan dalam distribusi.

Beberapa aplikasi umum z-score antara lain:

• Membandingkan skor tes siswa dari sekolah atau sistem pendidikan yang berbeda
• Menilai kinerja saham, obligasi, atau instrumen keuangan lainnya
• Mengevaluasi kinerja atlet dalam olahraga atau kompetisi yang berbeda
• Mendeteksi peristiwa atau kejadian yang tidak biasa dalam berbagai industri, seperti manufaktur atau kesehatan

Menghitung Z-Score

Untuk menghitung z-score dari suatu titik data, ikuti langkah-langkah berikut:

1. Tentukan rerata (\mu) dari distribusi.
2. Hitung standar deviasi (\sigma) dari distribusi.
3. Kurangi rerata dari titik data individu (X - \mu).
4. Bagi hasil dari langkah 3 dengan standar deviasi (\sigma).

Nilai yang dihasilkan mewakili z-score dari titik data, yang dapat digunakan untuk menentukan posisi relatifnya dalam distribusi dan membandingkannya dengan titik data atau distribusi lainnya.

Visualisasi Z-Score dengan Python

Di bab ini, saya akan menunjukkan cara memvisualisasikan z-score menggunakan Python. Kita akan membuat dataset acak dan menghitung z-score dari titik data. Kemudian, kita akan membuat plot data dan menyoroti 5% teratas dari titik data dengan matplotlib dan seaborn.

Pertama, kita perlu membuat dataset acak dan menghitung z-score dari titik datanya. Kita akan menggunakan numpy untuk tugas-tugas ini.

import numpy as np

# Generate a random dataset of 1000 normally distributed data points
np.random.seed(42)
data = np.random.normal(loc=50, scale=10, size=1000)

# Calculate mean and standard deviation
mean = np.mean(data)
std_dev = np.std(data)

# Calculate z-scores
z_scores = (data - mean) / std_dev

# Calculate the threshold for the top 5% (95th percentile)
threshold = np.percentile(z_scores, 95)

Sekarang setelah kita telah menghitung z-score untuk titik data, kita dapat memvisualisasikannya menggunakan matplotlib dan seaborn.

import matplotlib.pyplot as plt
import seaborn as sns

# Set seaborn plot style
sns.set(style="whitegrid")

# Create a scatter plot of the data points
plt.figure(figsize=(12, 6))
plt.scatter(data, z_scores, c="blue", label="Data points")

# Highlight the top 5% of data points in red
top_5_percent = data[z_scores >= threshold]
top_5_percent_z_scores = z_scores[z_scores >= threshold]
plt.scatter(top_5_percent, top_5_percent_z_scores, c="red", label="Top 5%")

# Add labels and title
plt.xlabel("Data Points")
plt.ylabel("Z-Scores")
plt.title("Z-Scores Visualization")

# Add a horizontal line representing the threshold for the top 5%
plt.axhline(y=threshold, linestyle="--", color="black", label=f"Threshold (Top 5%): {threshold:.2f}")

# Add a legend
plt.legend()

# Show the plot
plt.show()

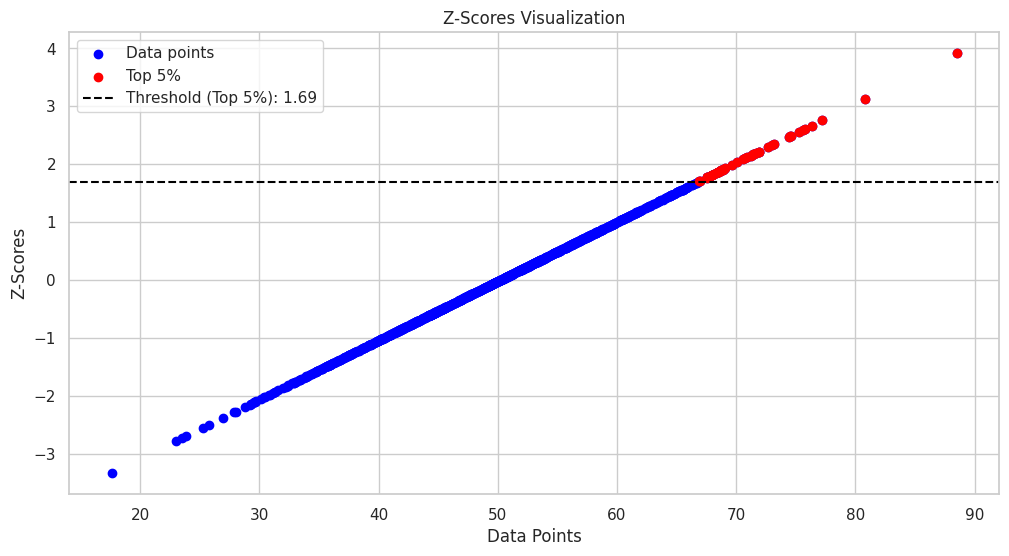
Kode ini akan menghasilkan plot titik tersebar dari titik data, dengan z-score yang sesuai pada sumbu y. 5% teratas dari titik data akan disorot dalam warna merah, dan garis putus menyiratkan ambang batas untuk 5% teratas akan ditambahkan ke plot.

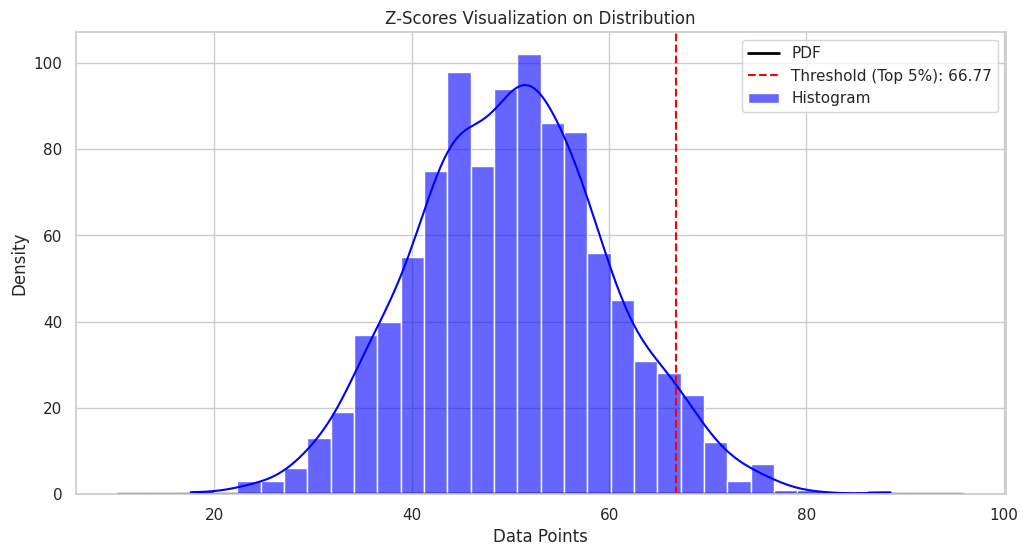
Untuk memvisualisasikan z-score pada distribusi, kita akan membuat histogram dan menimpanya dengan plot fungsi densitas probabilitas (PDF).

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import scipy.stats as stats

# Set seaborn plot style
sns.set(style="whitegrid")

# Create a histogram and PDF plot
plt.figure(figsize=(12, 6))
sns.histplot(data, kde=True, bins=30, color="blue", label="Histogram", alpha=0.6)
sns.kdeplot(data, color="black", linewidth=2, label="PDF")

# Calculate the data point corresponding to the 95th percentile threshold
threshold_data_point = mean + threshold * std_dev

# Add a vertical line representing the threshold for the top 5%
plt.axvline(x=threshold_data_point, linestyle="--", color="red", label=f"Threshold (Top 5%): {threshold_data_point:.2f}")

# Add labels and title
plt.xlabel("Data Points")
plt.ylabel("Density")
plt.title("Z-Scores Visualization on Distribution")

# Add a legend
plt.legend()

# Show the plot
plt.show()

Plot yang dihasilkan akan menunjukkan distribusi titik data dan ambang batas z-score untuk 5% teratas dari titik data.