2023-02-17

NLP 100 Exercise bab 8：Neral Networks

Machine Learning

NLP

Pengantar

Tokyo Institute of Technology telah menciptakan dan memelihara koleksi latihan NLP yang disebut "NLP 100 Exercise".

https://nlp100.github.io/en/ch08.html

Dalam artikel ini, saya akan memberikan contoh jawaban untuk "Chapter 8: Neural Networks".

70. Generating Features through Word Vector Summation

Mari kita pertimbangkan untuk mengubah dataset dari masalah 50 menjadi vektor fitur. Sebagai contoh, kita ingin membuat sebuah matriks $X$ (urutan vektor fitur dari semua contoh) dan sebuah vektor $Y$ (urutan label emas dari semua contoh).

X = \begin{pmatrix} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \\ \dots \\ \boldsymbol{x}_n \\ \end{pmatrix} \in \mathbb{R}^{n \times d}, Y = \begin{pmatrix} y_1 \\ y_2 \\ \dots \\ y_n \\ \end{pmatrix} \in \mathbb{N}^{n}

Di sini, n mewakili sejumlah contoh dalam data pelatihan. $\boldsymbol x_i \in \mathbb{R}^d$ dan $y_i \in \mathbb N$ masing-masing mewakili vektor fitur ke- $i \in \{1, \dots, n\}$ dan label target (emas). Perhatikan bahwa tugasnya adalah mengklasifikasikan judul yang diberikan ke dalam salah satu dari empat kategori berikut: "Business", "Science", "Entertainment", dan "Health". Mari kita definisikan bahwa $\mathbb N_4$ merepresentasikan sebuah bilangan asli yang lebih kecil dari 4 (termasuk nol). Kemudian label emas dari sebuah contoh dapat direpresentasikan sebagai $y_i \in \mathbb N_4$ . Mari kita juga mendefinisikan bahwa L merepresentasikan jumlah label (kali ini L=4).

Vektor fitur dari contoh ke- $i$ $x_i$ dihitung sebagai berikut:

\boldsymbol x_i = \frac{1}{T_i} \sum_{t=1}^{T_i} \mathrm{emb}(w_{i,t})

di mana $i$ -th instance terdiri dari token $T_i$ $(w_{i,1}, w_{i,2}, \dots, w_{i,T_i})$ dan $\mathrm{emb}(w)\in \mathbb{R}^d$ merepresentasikan sebuah vektor kata (ukuran $d$ ) yang sesuai dengan kata $w$ . Dengan kata lain, judul artikel ke- $i$ direpresentasikan sebagai rata-rata vektor kata dari semua kata dalam judul. Untuk penyematan kata, gunakan vektor kata yang sudah dilatih dengan dimensi 300 (yaitu, $d=300$ ).

Label emas dari instance ke- $i$ ke- $y_i$ didefinisikan sebagai berikut:

y_i = \begin{cases} 0 & (\textrm{if article }\boldsymbol x_i\textrm{ belong to Business category}) \\ 1 & (\textrm{if article }\boldsymbol x_i\textrm{ belong to Science category}) \\ 2 & (\textrm{if article }\boldsymbol x_i\textrm{ belong to Entertainment category}) \\ 3 & (\textrm{if article }\boldsymbol x_i\textrm{ belong to Health category}) \\ \end{cases}

Perhatikan bahwa Anda tidak harus mengikuti definisi di atas secara ketat selama ada pemetaan satu-ke-satu antara nama kategori dan indeks label.

Berdasarkan spesifikasi di atas, buatlah matriks dan vektor berikut ini dan simpanlah ke dalam file biner:

Training data feature matrix: $X_{\rm train} \in \mathbb{R}^{N_t \times d}$

Training data label matrix: $Y_{\rm train} \in \mathbb{N}^{N_t}$

Validation data feature matrix: $X_{\rm valid} \in \mathbb{R}^{N_v \times d}$

Validation data label matrix: $Y_{\rm valid} \in \mathbb{N}^{N_v}$

Test data feature matrix: $X_{\rm test} \in \mathbb{R}^{N_e \times d}$

Test data label matrix: $Y_{\rm test} \in \mathbb{N}^{N_e}$

Di sini, $N_t$ , $N_v$ , $N_e$ masing-masing mewakili jumlah contoh dalam data pelatihan, data validasi, dan data uji.

!wget https://archive.ics.uci.edu/ml/machine-learning-databases/00359/NewsAggregatorDataset.zip
!unzip NewsAggregatorDataset.zip

import pandas as pd
from sklearn.model_selection import train_test_split
from gensim.models import KeyedVectors
import string
import torch

df = pd.read_csv('./newsCorporay.csv',
                 header=None,
                 sep='\t',
                 names=['ID', 'TITLE', 'URL', 'PUBLISHER', 'CATEGORY', 'STORY', 'HOSTNAME', 'TIMESTAMP']
                 )

df = df.loc[df['PUBLISHER'].isin(['Reuters', 'Huffington Post', 'Businessweek', 'Contactmusic.com', 'Daily Mail']), ['TITLE', 'CATEGORY']]

# split data
train, valid_test = train_test_split(
    df,
    test_size=0.2,
    shuffle=True,
    random_state=42,
    stratify=df['CATEGORY']
)
valid, test = train_test_split(
    valid_test,
    test_size=0.5,
    shuffle=True,
    random_state=42,
    stratify=valid_test['CATEGORY']
)

model = KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin.gz', binary=True)

def w2v(text):
  words = text.translate(str.maketrans(string.punctuation, ' '*len(string.punctuation))).split()
  vec = [model[word] for word in words if word in model]
  return torch.tensor(sum(vec) / len(vec))

# create x vectors
X_train = torch.stack([w2v(text) for text in train['TITLE']])
X_valid = torch.stack([w2v(text) for text in valid['TITLE']])
X_test = torch.stack([w2v(text) for text in test['TITLE']])

# create y vectors
category_dict = {'b': 0, 't': 1, 'e':2, 'm':3}
y_train = torch.tensor(train['CATEGORY'].map(lambda x: category_dict[x]).values)
y_valid = torch.tensor(valid['CATEGORY'].map(lambda x: category_dict[x]).values)
y_test = torch.tensor(test['CATEGORY'].map(lambda x: category_dict[x]).values)

# save
torch.save(X_train, 'X_train.pt')
torch.save(X_valid, 'X_valid.pt')
torch.save(X_test, 'X_test.pt')
torch.save(y_train, 'y_train.pt')
torch.save(y_valid, 'y_valid.pt')
torch.save(y_test, 'y_test.pt')

71. Building Single Layer Neural Network

Muat matriks dan vektor dari soal 70. Hitung operasi-operasi berikut ini pada data pelatihan:

\hat{y}_1=softmax(x_1W),\\\hat{Y}=softmax(X_{[1:4]}W)

Di sini, softmax mengacu pada fungsi softmax dan $X_{[1:4]}∈\mathbb{R}^{4×d}$ adalah gabungan vertikal dari $x_1$ , $x_2$ , $x_3$ , $x_4$ :

X_{[1:4]}=\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}

Matriks $W \in \mathbb{R}^{d \times L}$ adalah bobot dari jaringan syaraf lapisan tunggal. Anda dapat menginisialisasi bobot secara acak untuk saat ini (k akan memperbarui parameternya di pertanyaan selanjutnya). Perhatikan bahwa $\hat{\boldsymbol y_1} \in \mathbb{R}^L$ merepresentasikan distribusi probabilitas atas kategori. Demikian pula, $\hat{Y} \in \mathbb{R}^{n \times L}$ merepresentasikan distribusi probabilitas dari setiap contoh pada data pelatihan $x_1, x_2, x_3, x_4$ .

from torch import nn

class SimpleNet(nn.Module):
  def __init__(self, input_size, output_size):
    super().__init__()
    self.fc = nn.Linear(input_size, output_size, bias=False)
    nn.init.normal_(self.fc.weight, 0.0, 1.0)

  def forward(self, x):
    x = self.fc(x)
    return x

model = SimpleNet(300, 4)

y1_hat = torch.softmax(model(X_train[0]), dim=-1)
print(y1_hat)
print('\n')
Y_hat = torch.softmax(model.forward(X_train[:4]), dim=-1)
print(Y_hat)


>> tensor([0.6961, 0.0492, 0.0851, 0.1696], grad_fn=<SoftmaxBackward0>)
>>
>> tensor([[0.6961, 0.0492, 0.0851, 0.1696],
>>         [0.5393, 0.0273, 0.3510, 0.0824],
>>         [0.7999, 0.0519, 0.1301, 0.0182],
>>         [0.3292, 0.1503, 0.1286, 0.3919]], grad_fn=<SoftmaxBackward0>)

72. Calculating loss and gradients

Hitung kerugian entropi silang dan gradien untuk matriks $W$ pada sampel pelatihan $x_1$ dan satu set sampel $x_1$ , $x_2$ , $x_3$ , $x_4$ . Kerugian pada sampel tunggal dihitung menggunakan rumus berikut:

l_i=−log[\textrm{probability that sample } x_i \textrm{ is classified as } y_i]

Kerugian entropi silang untuk sekumpulan sampel adalah rata-rata dari kerugian setiap sampel yang termasuk dalam kumpulan tersebut.

criterion = nn.CrossEntropyLoss()

loss_1 = criterion(model(X_train[0]), y_train[0])
model.zero_grad()
loss_1.backward()
print(f'loss: {loss_1:.3f}')
print(f'gradient:\n{model.fc.weight.grad}')

loss = criterion(model(X_train[:4]), y_train[:4])
model.zero_grad()
loss.backward()
print(f'loss: {loss:.3f}')
print(f'gradient:\n{model.fc.weight.grad}')

>>loss: 2.074
>>gradient:
>>tensor([[ 0.0010,  0.0071,  0.0020,  ..., -0.0181,  0.0040,  0.0138],
>>        [ 0.0010,  0.0073,  0.0021,  ..., -0.0185,  0.0041,  0.0141],
>>        [-0.0075, -0.0549, -0.0157,  ...,  0.1400, -0.0308, -0.1068],
>>        [ 0.0055,  0.0406,  0.0116,  ..., -0.1034,  0.0228,  0.0789]])
>>
>>loss: 2.796
>>gradient:
>>tensor([[ 0.0241, -0.0344, -0.0255,  ..., -0.0221, -0.0253, -0.0218],
>>        [-0.0181,  0.0021,  0.0147,  ..., -0.0224, -0.0172,  0.0403],
>>        [-0.0018, -0.0030, -0.0008,  ...,  0.0443,  0.0063, -0.0327],
>>        [-0.0042,  0.0352,  0.0116,  ...,  0.0002,  0.0363,  0.0143]])

73. Learning with stochastic gradient descent

Perbarui matriks $W$ menggunakan stochastic gradient descent (SGD). Pelatihan harus diakhiri dengan kriteria yang sesuai, misalnya, "berhenti setelah 100 epoch".

class Dataset(torch.utils.data.Dataset):
  def __init__(self, X, y):
    self.X = X
    self.y = y
    self.size = len(y)

  def __len__(self):
    return self.size

  def __getitem__(self, index):
    return [self.X[index], self.y[index]]

# create Dataset
train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)
test_ds = Dataset(X_test, y_test)

# create Dataloader
train_dl = torch.utils.data.DataLoader(train_ds,
                                       batch_size=1,
                                       shuffle=True
                                       )
valid_dl = torch.utils.data.DataLoader(valid_ds,
                                       batch_size=len(valid_ds),
                                       shuffle=False
                                       )
test_dl = torch.utils.data.DataLoader(test_ds,
                                      batch_size=len(test_ds),
                                      shuffle=False
                                      )

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
for epoch in range(num_epochs):
  model.train()
  loss_train = 0.0
  for i, (inputs, labels) in enumerate(train_dl):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()
    loss_train += loss.item()

  loss_train = loss_train / i
  model.eval()
  with torch.no_grad():
    inputs, labels = next(iter(valid_dl))
    outputs = model(inputs)
    loss_valid = criterion(outputs, labels)

  print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, loss_valid: {loss_valid:.3f}')

>> epoch: 1, loss_train: 0.471, loss_valid: 0.367
>> epoch: 2, loss_train: 0.309, loss_valid: 0.335
>> epoch: 3, loss_train: 0.281, loss_valid: 0.320
>> epoch: 4, loss_train: 0.265, loss_valid: 0.314
>> epoch: 5, loss_train: 0.256, loss_valid: 0.307
>> epoch: 6, loss_train: 0.250, loss_valid: 0.308
>> epoch: 7, loss_train: 0.244, loss_valid: 0.304
>> epoch: 8, loss_train: 0.240, loss_valid: 0.305
>> epoch: 9, loss_train: 0.237, loss_valid: 0.303
>> epoch: 10, loss_train: 0.234, loss_valid: 0.305

74. Measuring accuracy

Hitunglah akurasi klasifikasi pada data pelatihan dan evaluasi dengan menggunakan matriks yang diperoleh pada soal 73.

def calc_accuracy(model, loader):
  model.eval()
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      outputs = model(inputs)
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()
  return correct / total

acc_train = calc_accuracy(model, train_dl)
acc_test = calc_accuracy(model, test_dl)
print(f'accuracy (train)：{acc_train:.3f}')
print(f'accuracy (test)：{acc_test:.3f}')

>> accuracy (train)：0.923
>> accuracy (test)：0.900

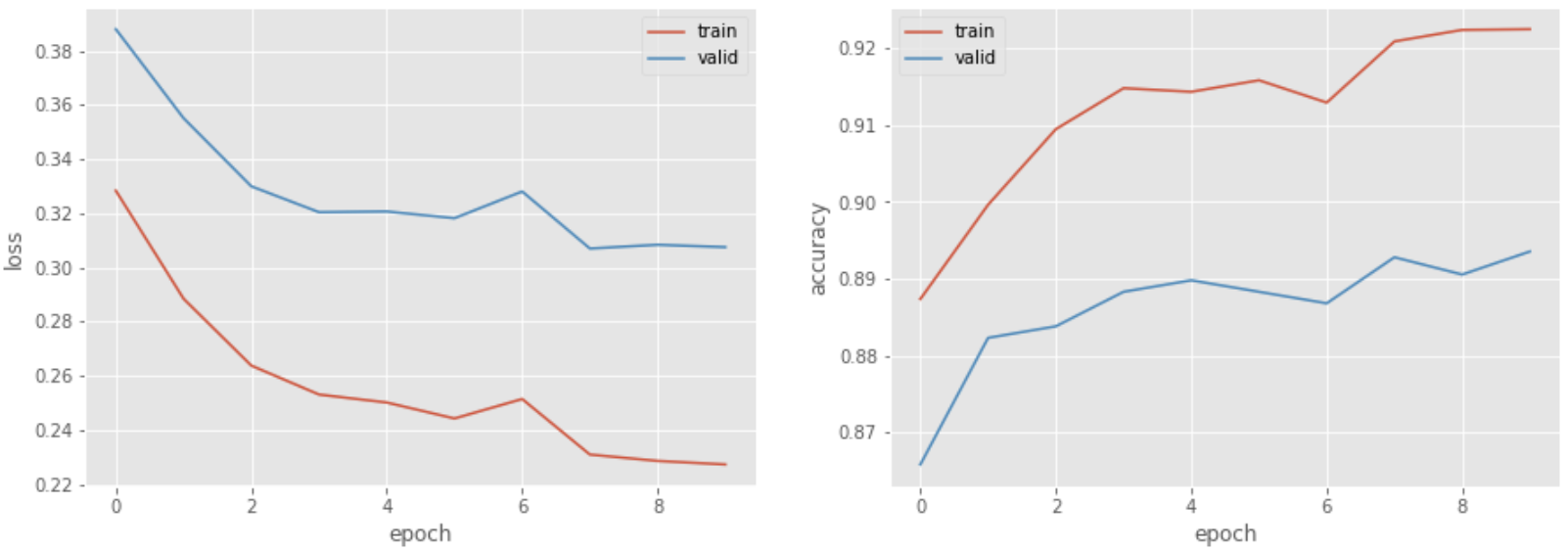
75. Plotting loss and accuracy

Modifikasi kode dari masalah 73 sehingga kerugian dan akurasi dari data pelatihan dan evaluasi diplot pada grafik setelah setiap epoch. Gunakan grafik ini untuk memantau kemajuan pembelajaran.

def calc_loss_and_accuracy(model, criterion, loader):
  model.eval()
  loss = 0.0
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      outputs = model(inputs)
      loss += criterion(outputs, labels).item()
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()
  return loss / len(loader), correct / total

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
log_train = []
log_valid = []
for epoch in range(num_epochs):
  model.train()
  for inputs, labels in train_dl:
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

  loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
  loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
  log_train.append([loss_train, acc_train])
  log_valid.append([loss_valid, acc_valid])

from matplotlib import pyplot as plt
import numpy as np

plt.style.use('ggplot')

fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log_train).T[0], label='train')
ax[0].plot(np.array(log_valid).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log_train).T[1], label='train')
ax[1].plot(np.array(log_valid).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()

76. Checkpoints

Modifikasi kode dari masalah 75 untuk menuliskan checkpoints ke sebuah file setelah setiap epoch. Checkpoints harus menyertakan nilai-nilai parameter seperti matriks bobot dan status internal algoritma optimasi.

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
log_train = []
log_valid = []
for epoch in range(num_epochs):
  model.train()
  for inputs, labels in train_dl:
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

  loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
  loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
  log_train.append([loss_train, acc_train])
  log_valid.append([loss_valid, acc_valid])

  torch.save({
                'epoch': epoch,
                'model_state_dict': model.state_dict(),
                'optimizer_state_dict': optimizer.state_dict()
             },
             f'checkpoint_{epoch + 1}.pt'
             )

77. Mini-batches

Modifikasi kode dari masalah 76 untuk menghitung loss/gradien dan perbarui nilai matriks $W$ untuk setiap sampel $B$ (batch mini). Bandingkan waktu yang dibutuhkan untuk satu epoch pembelajaran dengan mengubah nilai $B$ menjadi $1,2,4,8,...$ .

import time

def train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, num_epochs):
  train_dl = torch.utils.data.DataLoader(train_ds, batch_size=batch_size, shuffle=True)
  valid_dl = torch.utils.data.DataLoader(valid_ds, batch_size=len(valid_ds), shuffle=False)

  log_train = []
  log_valid = []
  for epoch in range(num_epochs):
    s_time = time.time()
    model.train()
    for inputs, labels in train_dl:
      optimizer.zero_grad()
      outputs = model(inputs)
      loss = criterion(outputs, labels)
      loss.backward()
      optimizer.step()

    loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
    loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
    log_train.append([loss_train, acc_train])
    log_valid.append([loss_valid, acc_valid])

    torch.save({
        'epoch': epoch,
        'model_state_dict': model.state_dict(),
        'optimizer_state_dict': optimizer.state_dict()
        },
        f'checkpoint_{epoch + 1}.pt'
    )

    e_time = time.time()

    print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, accuracy_train: {acc_train:.3f}, loss_valid: {loss_valid:.3f}, accuracy_valid: {acc_valid:.3f}, {(e_time - s_time):.3f}sec')

  return {'train': log_train, 'valid': log_valid}

train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

for batch_size in [2 ** i for i in range(11)]:
  print(f'batch size: {batch_size}')
  log = train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, 1)

>> batch size: 1
>> epoch: 1, loss_train: 0.337, accuracy_train: 0.884, loss_valid: 0.385, accuracy_valid: 0.869, 3.993sec
>> batch size: 2
>> epoch: 1, loss_train: 0.303, accuracy_train: 0.896, loss_valid: 0.348, accuracy_valid: 0.879, 2.457sec
>> batch size: 4
>> epoch: 1, loss_train: 0.292, accuracy_train: 0.899, loss_valid: 0.341, accuracy_valid: 0.881, 1.220sec
>> batch size: 8
>> epoch: 1, loss_train: 0.288, accuracy_train: 0.901, loss_valid: 0.337, accuracy_valid: 0.887, 0.802sec
>> batch size: 16
>> epoch: 1, loss_train: 0.286, accuracy_train: 0.901, loss_valid: 0.336, accuracy_valid: 0.887, 0.592sec
>> batch size: 32
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.902, loss_valid: 0.334, accuracy_valid: 0.886, 0.396sec
>> batch size: 64
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.307sec
>> batch size: 128
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.246sec
>> batch size: 256
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.219sec
>> batch size: 512
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.195sec
>> batch size: 1024
>> epoch: 1, loss_train: 0.287, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.198sec

78. Training on a GPU

Modifikasi kode dari masalah 77 sehingga dapat berjalan pada GPU.

def calc_loss_and_accuracy(model, criterion, loader, device):
  model.eval()
  loss = 0.0
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      inputs = inputs.to(device)
      labels = labels.to(device)
      outputs = model(inputs)
      loss += criterion(outputs, labels).item()
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()

  return loss / len(loader), correct / total


def train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, num_epochs, device=None):
  model.to(device)

  train_dl = torch.utils.data.DataLoader(train_ds,
                                         batch_size=batch_size,
                                         shuffle=True)
  valid_dl = torch.utils.data.DataLoader(valid_ds,
                                         batch_size=len(valid_ds),
                                         shuffle=False)

  log_train = []
  log_valid = []
  for epoch in range(num_epochs):
    s_time = time.time()
    model.train()
    for inputs, labels in train_dl:
      optimizer.zero_grad()
      inputs = inputs.to(device)
      labels = labels.to(device)
      outputs = model.forward(inputs)
      loss = criterion(outputs, labels)
      loss.backward()
      optimizer.step()

    loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl, device)
    loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl, device)
    log_train.append([loss_train, acc_train])
    log_valid.append([loss_valid, acc_valid])

    torch.save({
        'epoch': epoch,
        'model_state_dict': model.state_dict(),
        'optimizer_state_dict': optimizer.state_dict()
        },
        f'checkpoint_{epoch + 1}.pt'
    )

    e_time = time.time()

    print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, accuracy_train: {acc_train:.3f}, loss_valid: {loss_valid:.3f}, accuracy_valid: {acc_valid:.3f}, {(e_time - s_time):.3f}sec')

  return {'train': log_train, 'valid': log_valid}

train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

device = torch.device('cuda')

for batch_size in [2 ** i for i in range(11)]:
  print(f'batch size: {batch_size}')
  log = train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, 1, device=device)

>> batch size: 1
>> epoch: 1, loss_train: 0.337, accuracy_train: 0.883, loss_valid: 0.392, accuracy_valid: 0.868, 13.139sec
>> batch size: 2
>> epoch: 1, loss_train: 0.300, accuracy_train: 0.898, loss_valid: 0.357, accuracy_valid: 0.882, 4.998sec
>> batch size: 4
>> epoch: 1, loss_train: 0.291, accuracy_train: 0.901, loss_valid: 0.349, accuracy_valid: 0.885, 2.623sec
>> batch size: 8
>> epoch: 1, loss_train: 0.287, accuracy_train: 0.901, loss_valid: 0.346, accuracy_valid: 0.882, 1.589sec
>> batch size: 16
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.902, loss_valid: 0.344, accuracy_valid: 0.886, 0.902sec
>> batch size: 32
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.544sec
>> batch size: 64
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.377sec
>> batch size: 128
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.292sec
>> batch size: 256
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.291sec
>> batch size: 512
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.145sec
>> batch size: 1024
>> epoch: 1, loss_train: 0.282, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.126sec

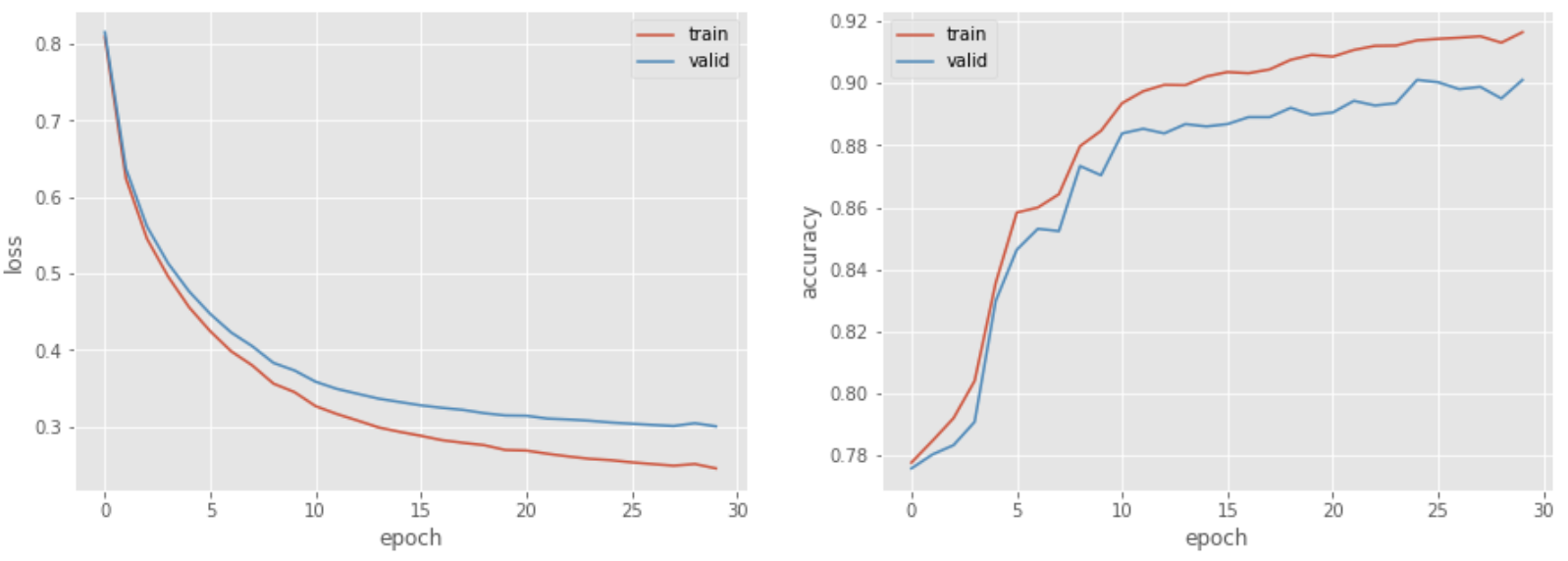
79. Multilayer Neural Networks

Modifikasi kode dari masalah 78 untuk membuat pengklasifikasi berkinerja tinggi dengan mengubah arsitektur jaringan saraf. Coba perkenalkan istilah bias dan beberapa lapisan.

from torch.nn import functional as F

class MLPNet(nn.Module):
  def __init__(self, input_size, mid_size, output_size):
    super().__init__()
    self.fc1 = nn.Linear(input_size, mid_size)
    self.act = nn.ReLU()
    self.fc2 = nn.Linear(mid_size, output_size)
    self.dropout = nn.Dropout(0.2)
    nn.init.kaiming_normal_(self.fc1.weight)
    nn.init.kaiming_normal_(self.fc2.weight)

  def forward(self, x):
    x = self.fc1(x)
    x = self.act(x)
    x = self.dropout(x)
    x = self.fc2(x)
    return x

model = MLPNet(300, 128, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

device = torch.device('cuda')

log = train_model(train_ds, valid_ds, 128, model, criterion, optimizer, 30, device=device)

fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log['train']).T[0], label='train')
ax[0].plot(np.array(log['valid']).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log['train']).T[1], label='train')
ax[1].plot(np.array(log['valid']).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()

>> epoch: 1, loss_train: 0.809, accuracy_train: 0.778, loss_valid: 0.815, accuracy_valid: 0.776, 0.247sec
>> epoch: 2, loss_train: 0.624, accuracy_train: 0.785, loss_valid: 0.637, accuracy_valid: 0.780, 0.429sec
>> epoch: 3, loss_train: 0.545, accuracy_train: 0.792, loss_valid: 0.561, accuracy_valid: 0.783, 0.278sec
>> epoch: 4, loss_train: 0.496, accuracy_train: 0.804, loss_valid: 0.513, accuracy_valid: 0.791, 0.241sec
>> epoch: 5, loss_train: 0.456, accuracy_train: 0.836, loss_valid: 0.477, accuracy_valid: 0.830, 0.248sec
>> epoch: 6, loss_train: 0.425, accuracy_train: 0.858, loss_valid: 0.447, accuracy_valid: 0.846, 0.244sec
>> epoch: 7, loss_train: 0.398, accuracy_train: 0.860, loss_valid: 0.423, accuracy_valid: 0.853, 0.247sec
>> epoch: 8, loss_train: 0.380, accuracy_train: 0.864, loss_valid: 0.405, accuracy_valid: 0.852, 0.251sec
>> epoch: 9, loss_train: 0.356, accuracy_train: 0.880, loss_valid: 0.383, accuracy_valid: 0.873, 0.263sec
>> epoch: 10, loss_train: 0.345, accuracy_train: 0.885, loss_valid: 0.373, accuracy_valid: 0.870, 0.260sec
>> epoch: 11, loss_train: 0.327, accuracy_train: 0.894, loss_valid: 0.359, accuracy_valid: 0.884, 0.243sec
>> epoch: 12, loss_train: 0.317, accuracy_train: 0.897, loss_valid: 0.349, accuracy_valid: 0.885, 0.246sec
>> epoch: 13, loss_train: 0.308, accuracy_train: 0.899, loss_valid: 0.343, accuracy_valid: 0.884, 0.260sec
>> epoch: 14, loss_train: 0.299, accuracy_train: 0.899, loss_valid: 0.336, accuracy_valid: 0.887, 0.241sec
>> epoch: 15, loss_train: 0.293, accuracy_train: 0.902, loss_valid: 0.332, accuracy_valid: 0.886, 0.237sec
>> epoch: 16, loss_train: 0.288, accuracy_train: 0.904, loss_valid: 0.328, accuracy_valid: 0.887, 0.247sec
>> epoch: 17, loss_train: 0.282, accuracy_train: 0.903, loss_valid: 0.325, accuracy_valid: 0.889, 0.239sec
>> epoch: 18, loss_train: 0.279, accuracy_train: 0.904, loss_valid: 0.322, accuracy_valid: 0.889, 0.252sec
>> epoch: 19, loss_train: 0.276, accuracy_train: 0.908, loss_valid: 0.318, accuracy_valid: 0.892, 0.241sec
>> epoch: 20, loss_train: 0.269, accuracy_train: 0.909, loss_valid: 0.315, accuracy_valid: 0.890, 0.241sec
>> epoch: 21, loss_train: 0.269, accuracy_train: 0.909, loss_valid: 0.314, accuracy_valid: 0.891, 0.240sec
>> epoch: 22, loss_train: 0.265, accuracy_train: 0.911, loss_valid: 0.311, accuracy_valid: 0.894, 0.251sec
>> epoch: 23, loss_train: 0.261, accuracy_train: 0.912, loss_valid: 0.309, accuracy_valid: 0.893, 0.243sec
>> epoch: 24, loss_train: 0.258, accuracy_train: 0.912, loss_valid: 0.308, accuracy_valid: 0.894, 0.237sec
>> epoch: 25, loss_train: 0.256, accuracy_train: 0.914, loss_valid: 0.305, accuracy_valid: 0.901, 0.240sec
>> epoch: 26, loss_train: 0.253, accuracy_train: 0.914, loss_valid: 0.304, accuracy_valid: 0.900, 0.244sec
>> epoch: 27, loss_train: 0.251, accuracy_train: 0.915, loss_valid: 0.302, accuracy_valid: 0.898, 0.236sec
>> epoch: 28, loss_train: 0.249, accuracy_train: 0.915, loss_valid: 0.301, accuracy_valid: 0.899, 0.239sec
>> epoch: 29, loss_train: 0.251, accuracy_train: 0.913, loss_valid: 0.304, accuracy_valid: 0.895, 0.241sec
>> epoch: 30, loss_train: 0.245, accuracy_train: 0.916, loss_valid: 0.300, accuracy_valid: 0.901, 0.241sec