2022-12-28

Model Logit Bertingkat

Statistics

Statistical Model

Discrete Choice Model

Apa itu Model Logit Bertingkat

Model logit bertingkat adalah suatu model pilihan diskrit yang memperluas model logit multinomial standar untuk memperhitungkan keberadaan kesamaan yang tidak diamati di antara alternatif keputusan. Model logit bertingkat dapat digunakan dalam situasi di mana asumsi Independence from Irrelevant Alternatives (IIA) tidak berlaku, yang merupakan keterbatasan utama dari model logit multinomial.

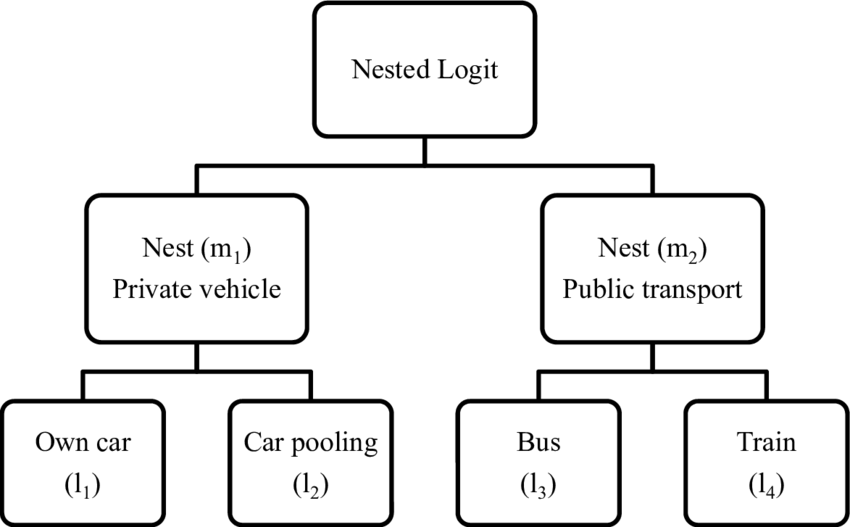
Model logit bertingkat menyusun alternatif ke dalam struktur bertingkat dari sarang, di mana setiap sarang berisi kumpulan alternatif yang mempunyai beberapa karakteristik umum yang tidak diamati.

Nested Logit Model
APPLICATION OF NEURAL NETWORK FOR MODE CHOICE MODELING AND MODAL TRAFFIC FORECASTING

Model logit bertingkat telah banyak diterapkan di berbagai bidang, termasuk pemodelan permintaan transportasi, analisis pangsa pasar dan pilihan produk, ekonomi lingkungan dan resource, dan ekonomi kesehatan. Topik lanjutan dan perluasan dari model logit bertingkat meliputi model logit bertingkat silang, model logit campuran, model kelas laten, dan model logit bertingkat data panel atau dinamis. Perluasan ini lebih meningkatkan fleksibilitas dan aplikabilitas kerangka kerja model logit bertingkat dalam menangani masalah pengambilan keputusan yang kompleks.

Dasar Teoritis Model Logit Bertingkat

Pembentukan Model Logit Bertingkat

Untuk membentuk model logit bertingkat, terlebih dahulu kita mengelompokkan alternatif ke dalam struktur bertingkat dari sarang. Setiap sarang berisi kumpulan alternatif yang mempunyai karakteristik umum yang tidak diamati. Proses pemilihan kemudian terjadi dalam dua tahap: pertama, individu memilih sarang, dan kemudian memilih alternatif di dalam sarang tersebut.

Misalkan $G$ adalah himpunan sarang, dan $J_g$ adalah himpunan alternatif di dalam sarang $g$ . Probabilitas individu $i$ memilih alternatif $j$ di dalam sarang $g$ dapat dinyatakan sebagai:

P_{ij} = P_i(j|g) \cdot P_i(g)

di mana $P_i(j|g)$ adalah probabilitas bersyarat memilih alternatif $j$ yang diberikan sarang $g$ , dan $P_i(g)$ adalah probabilitas memilih sarang $g$ .

Dengan mengadopsi kerangka kerja RUM dan mengasumsikan bahwa komponen acak dari utilitas mengikuti distribusi Gumbel, kita dapat membentuk model logit bertingkat:

P_{ij} = \frac{\exp\left(\frac{V_{ij}}{\tau_g}\right)}{\sum_{j' \in J_g} \exp\left(\frac{V_{i(j')}}{\tau_g}\right)} \cdot \frac{\left(\sum_{j \in J_g} \exp\left(\frac{V_{ij}}{\tau_g}\right)\right)^{(1 - \tau_g)}}{\sum_{g' \in G} \sum_{j' \in J_{(g')}} \exp\left(\frac{V_{i(j')}}{\tau_{(g')}}\right)^{(1 - \tau_{(g')})}}

di mana $\tau_g$ adalah parameter ketidakserupaannya untuk sarang $g$ , yang mengukur derajat korelasi di antara alternatif di dalam sarang yang sama. Istilah $\sum_{j \in J_g} \exp\left(\frac{V_{ij}}{\tau_g}\right)$ dikenal sebagai nilai inklusif untuk sarang $g$ .

Nilai Inklusif dan Parameter Ketidakserupaannya

Nilai inklusif untuk sarang $g$ mewakili utilitas maksimum yang diharapkan di dalam sarang tersebut. Hal ini memainkan peran penting dalam menghitung probabilitas memilih sarang tertentu. Nilai inklusif yang lebih tinggi menunjukkan probabilitas yang lebih besar untuk memilih sarang tertentu.

Parameter ketidakserupaan, $\tau_g$ , mengukur derajat korelasi di antara alternatif di dalam sarang. Ketika $\tau_g$ sama dengan 1, model logit bertingkat menyamai model logit multinomial, dan asumsi IIA berlaku. Ketika $\tau_g$ mendekati 0, alternatif di dalam sarang menjadi lebih serupa, dan korelasi di antara mereka meningkat. Penting untuk diingat bahwa parameter ketidakserupaan harus berada di antara 0 dan 1 agar model konsisten dengan maksimalisasi utilitas.

Bab ini telah mempresentasikan dasar teoritis dari model logit bertingkat, termasuk konsep IIA, Random Utility Maximization, pembentukan model logit bertingkat, dan peran nilai inklusif dan parameter ketidakserupaannya.

Model Logit Bertingkat dengan R

Pada bab ini, saya akan menunjukkan contoh bagaimana memperkirakan model logit bertingkat menggunakan R. Kita akan menggunakan paket mlogit, yang mendukung estimasi dari berbagai model pilihan diskret, termasuk model logit bertingkat. Kita akan menggunakan kumpulan data TravelMode dari paket AER sebagai contoh dataset.

Kumpulan data TravelMode berisi informasi tentang pilihan yang dibuat oleh individu ketika memilih mode transportasi. Dataset memiliki variabel sebagai berikut:

id: identifikasi individu
mode: mode transportasi (udara, kereta api, mobil, atau bus)
choice: variabel biner yang menunjukkan mode yang dipilih (1 untuk dipilih, 0 sebaliknya)
gcost: biaya umum mode transportasi
wait: waktu tunggu mode transportasi

Persiapan Data

Pasang paket dan muat dataset TravelMode.

# Install mlogit and AER packages and load them. Latter is just for a dataset we'll be using.
# install.packages("mlogit", "AER")
library("mlogit", "AER")

# Load dataset TravelMode
data("TravelMode", package = "AER")

Mari kita tampilkan tabelnya.

show(TravelMode)

    individual  mode choice wait vcost travel gcost income size
1            1   air     no   69    59    100    70     35    1
2            1 train     no   34    31    372    71     35    1
3            1   bus     no   35    25    417    70     35    1
4            1   car    yes    0    10    180    30     35    1
5            2   air     no   64    58     68    68     30    2
6            2 train     no   44    31    354    84     30    2
7            2   bus     no   53    25    399    85     30    2
8            2   car    yes    0    11    255    50     30    2
9            3   air     no   69   115    125   129     40    1
10           3 train     no   34    98    892   195     40    1
11           3   bus     no   35    53    882   149     40    1
12           3   car    yes    0    23    720   101     40    1

Estimasi Model

Perkirakan model logit bertingkat.

# Use the mlogit() function to run a nested logit estimation

# Here, we will predict what mode of travel individuals
# choose using cost and wait times

nested_logit_model = mlogit(
  choice ~ gcost + wait,
  data = TravelMode,
  ##The variable from which our nests are determined
  alt.var = 'mode',
  #The variable that dictates the binary choice
  choice = 'choice',
  #List of nests as named vectors
  nests = list(fast = c('air','train'), slow = c('car','bus'))
  )

alt.var = 'mode'
Argumen ini menentukan nama variabel dalam dataset yang berisi alternatif yang berbeda (mode transportasi dalam hal ini). Di sini, alternatif disimpan dalam variabel 'mode'.
choice = 'choice'
Argumen ini menentukan nama variabel dalam dataset yang menunjukkan apakah alternatif dipilih (1) atau tidak (0). Dalam hal ini, variabel pilihan biner disebut 'choice'.
nests = list(fast = c('air','train'), slow = c('car','bus'))
Argumen ini mendefinisikan sarang-sarang untuk model logit bertingkat. Sarang-sarang ini ditentukan sebagai daftar vektor bernama, di mana setiap vektor berisi alternatif yang termasuk dalam sarang tertentu. Dalam hal ini, terdapat dua sarang: 'fast' (yang berisi 'air' dan 'train') dan 'slow' (yang berisi 'car' dan 'bus').

Objek nested_logit_model yang dihasilkan dapat digunakan untuk memperoleh berbagai statistik model dengan memanggil fungsi summary() padanya.

# The results
summary(nested_logit_model)

Call:
mlogit(formula = choice ~ gcost + wait, data = TravelMode, nests = list(fast = c("air",
    "train"), slow = c("car", "bus")), alt.var = "mode", choice = "choice")

Frequencies of alternatives:choice
    air   train     bus     car
0.27619 0.30000 0.14286 0.28095

bfgs method
15 iterations, 0h:0m:0s
g'(-H)^-1g = 2.04E-07
gradient close to zero

Coefficients :
                    Estimate Std. Error z-value  Pr(>|z|)
(Intercept):train -2.6632486  0.8797054 -3.0274  0.002466 **
(Intercept):bus   -2.9341306  0.9247620 -3.1728  0.001510 **
(Intercept):car   -8.0988987  1.8709536 -4.3288 1.500e-05 ***
gcost             -0.0234085  0.0059397 -3.9410 8.115e-05 ***
wait              -0.1499260  0.0364437 -4.1139 3.890e-05 ***
iv:fast            2.3918823  0.9701086  2.4656  0.013679 *
iv:slow            0.9745729  0.3598853  2.7080  0.006769 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Log-Likelihood: -189.74
McFadden R^2:  0.33132
Likelihood ratio test : chisq = 188.03 (p.value = < 2.22e-16)

Berikut ini adalah interpretasi hasil dari model logit bertingkat:

Frequencies of alternatives
Frekuensi menunjukkan proporsi dari setiap mode transportasi yang dipilih dalam dataset. Dalam hal ini, udara dipilih oleh 27,62% individu, kereta api oleh 30,00%, bus oleh 14,29%, dan mobil oleh 28,10%. Nilai ini memberikan pemahaman dasar tentang popularitas setiap mode.
Coefficients
Koefisien mewakili hubungan antara variabel prediktor dan log odds memilih mode transportasi tertentu relatif terhadap kategori referensi (dalam hal ini, mode udara). Koefisien positif menunjukkan peningkatan dalam log odds memilih mode, sedangkan koefisien negatif menunjukkan penurunan.
(Intercept):train, (Intercept):bus, dan (Intercept):car
Ini adalah konstanta yang spesifik untuk alternatif kereta api, bus, dan mobil, masing-masing. Ini mewakili log odds dasar memilih setiap mode relatif terhadap mode udara ketika semua variabel prediktor nol. Koefisien negatif untuk ketiga alternatif menunjukkan bahwa log odds memilih masing-masing mode lebih rendah daripada memilih udara, dengan nilai variabel prediktor yang sama.
gcost
Biaya umum memiliki koefisien negatif (-0,0234), yang menunjukkan bahwa ketika biaya umum suatu mode transportasi meningkat, kemungkinan memilih mode tersebut akan menurun. Hasil ini signifikan secara statistik, seperti yang ditunjukkan oleh nilai p yang rendah (8,115e-05).
wait
Waktu tunggu juga memiliki koefisien negatif (-0,1499), yang berarti bahwa ketika waktu tunggu untuk mode transportasi meningkat, kemungkinan memilih mode tersebut akan menurun. Hasil ini signifikan secara statistik juga, dengan nilai p sebesar 3,890e-05.
Parameter nilai inklusif (iv)
Parameter nilai inklusif mewakili perbedaan antara alternatif dalam masing-masing sarang. Koefisien positif dan signifikan secara statistik untuk kedua sarang (iv:fast = 2,3919, nilai p = 0,0137 dan iv:slow = 0,9746, nilai p = 0,0068) menunjukkan bahwa faktor-faktor yang tidak diamati yang mempengaruhi pilihan alternatif dalam sarang-sarang ini berkorelasi positif.
Log-Likelihood
Nilai log-likelihood sebesar -189,74 adalah ukuran seberapa baik model cocok dengan data. Nilai yang lebih tinggi menunjukkan kecocokan yang lebih baik.
McFadden R^2
Nilai McFadden R^2 sebesar 0,3313 adalah ukuran kecocokan model. Rentang nilainya dari 0 hingga 1, dengan nilai yang lebih tinggi menunjukkan kecocokan yang lebih baik. Nilai ini menunjukkan bahwa model menjelaskan sekitar 33,13% variasi dalam data.
Likelihood ratio test
Statistik uji rasio kemungkinan (chisq = 188,03) dan nilai p (<2,22e-16) menunjukkan bahwa model ini secara statistik signifikan dan merupakan peningkatan dari model tanpa variabel prediktor.

Secara keseluruhan, hasil dari model logit bertingkat menunjukkan bahwa baik biaya umum maupun waktu tunggu mempengaruhi secara negatif pilihan mode transportasi, dengan individu cenderung memilih alternatif dengan biaya yang lebih rendah dan waktu tunggu yang lebih singkat. Selain itu, parameter nilai inklusif yang positif dan signifikan menunjukkan bahwa terdapat korelasi antara faktor-faktor yang tidak diamati yang mempengaruhi pilihan alternatif dalam masing-masing sarang (mode transportasi yang fast dan slow).