2022-12-28

Nested Logit Model

Statistics

Statistical Model

Discrete Choice Model

What is Nested Logit Model

The nested logit model is a discrete choice model that extends the standard multinomial logit model to account for the presence of unobserved similarities among decision alternatives. Nested logit models can be used in situations where the Independence from Irrelevant Alternatives (IIA) assumption does not hold, which is a key limitation of the multinomial logit model.

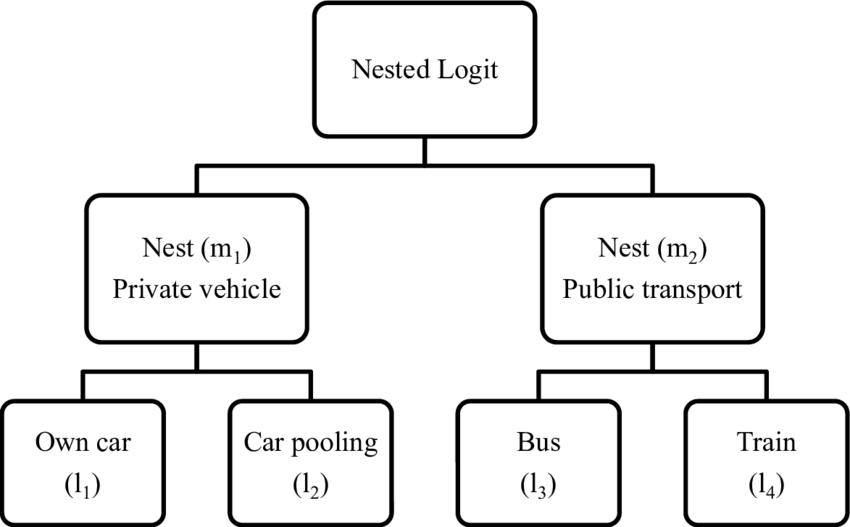
Nested logit models arrange alternatives into a hierarchical structure of nests, where each nest contains a set of alternatives that share some unobserved common characteristics.

Nested Logit Model
APPLICATION OF NEURAL NETWORK FOR MODE CHOICE MODELING AND MODAL TRAFFIC FORECASTING

Nested logit models have been widely applied across various fields, including transportation demand modeling, market share analysis and product choice, environmental and resource economics, and health economics. Advanced topics and extensions of the nested logit model include cross-nested logit models, mixed logit models, latent class models, and panel data or dynamic nested logit models. These extensions further enhance the flexibility and applicability of the nested logit framework in addressing complex decision-making problems.

Theoretical Foundations of Nested Logit Models

Derivation of the Nested Logit Model

To derive the nested logit model, we first group alternatives into a hierarchical structure of nests. Each nest contains a set of alternatives that share unobserved common characteristics. The choice process then occurs in two stages: first, individuals choose a nest, and then they choose an alternative within that nest.

Let $G$ be the set of nests, and let $J_g$ be the set of alternatives within nest $g$ . The probability of individual $i$ choosing alternative $j$ in nest $g$ can be expressed as:

P_{ij} = P_i(j|g) \cdot P_i(g)

where $P_i(j|g)$ is the conditional probability of choosing alternative $j$ given nest $g$ , and $P_i(g)$ is the probability of choosing nest $g$ .

By adopting the Random Utility Maximization and assuming that the random component of utility follows a Gumbel distribution, we can derive the nested logit model:

P_{ij} = \frac{\exp\left(\frac{V_{ij}}{\tau_g}\right)}{\sum_{j' \in J_g} \exp\left(\frac{V_{i(j')}}{\tau_g}\right)} \cdot \frac{\left(\sum_{j \in J_g} \exp\left(\frac{V_{ij}}{\tau_g}\right)\right)^{(1 - \tau_g)}}{\sum_{g' \in G} \sum_{j' \in J_{(g')}} \exp\left(\frac{V_{i(j')}}{\tau_{(g')}}\right)^{(1 - \tau_{(g')})}}

where $\tau_g$ is the dissimilarity parameter for nest $g$ , which measures the degree of correlation among alternatives within the same nest. The term $\sum_{j \in J_g} \exp\left(\frac{V_{ij}}{\tau_g}\right)$ is known as the inclusive value for nest $g$ .

Inclusive Value and Dissimilarity Parameters

The inclusive value for nest $g$ represents the expected maximum utility within that nest. It plays a crucial role in computing the probability of choosing a specific nest. A higher inclusive value indicates a greater probability of choosing a particular nest.

The dissimilarity parameter, $\tau_g$ , measures the degree of correlation among alternatives within a nest. When $\tau_g$ equals 1, the nested logit model reduces to the multinomial logit model, and the IIA assumption holds. As $\tau_g$ approaches 0, the alternatives within the nest become more similar, and the correlations among them increase. It is important to note that the dissimilarity parameter should lie between 0 and 1 for the model to be consistent with utility maximization.

This chapter has presented the theoretical foundations of nested logit models, including the concepts of IIA, the Random Utility Maximization, the derivation of the nested logit model, and the role of inclusive value and dissimilarity parameters.

Nested Logit Model with R

In this chapter, I will demonstrate an example of how to estimate a nested logit model using R. We will use the mlogit package, which supports the estimation of various discrete choice models, including nested logit models. We will use the TravelMode dataset from the AER package as our example dataset.

The TravelMode dataset contains information on the choices made by individuals when selecting a mode of transportation. The dataset has the following variables:

id: the individual identifier
mode: the mode of transportation (air, train, car, or bus)
choice: a binary variable indicating the chosen mode (1 for chosen, 0 otherwise)
gcost: the generalized cost of the transportation mode
wait: the waiting time for the transportation mode

Preparing Data

Install packages and load TravelMode dataset.

# Install mlogit and AER packages and load them. Latter is just for a dataset we'll be using.
# install.packages("mlogit", "AER")
library("mlogit", "AER")

# Load dataset TravelMode
data("TravelMode", package = "AER")

Let's show the table.

show(TravelMode)

    individual  mode choice wait vcost travel gcost income size
1            1   air     no   69    59    100    70     35    1
2            1 train     no   34    31    372    71     35    1
3            1   bus     no   35    25    417    70     35    1
4            1   car    yes    0    10    180    30     35    1
5            2   air     no   64    58     68    68     30    2
6            2 train     no   44    31    354    84     30    2
7            2   bus     no   53    25    399    85     30    2
8            2   car    yes    0    11    255    50     30    2
9            3   air     no   69   115    125   129     40    1
10           3 train     no   34    98    892   195     40    1
11           3   bus     no   35    53    882   149     40    1
12           3   car    yes    0    23    720   101     40    1

Model Estimation

Estimate the nested logit model.

# Use the mlogit() function to run a nested logit estimation

# Here, we will predict what mode of travel individuals
# choose using cost and wait times

nested_logit_model = mlogit(
  choice ~ gcost + wait,
  data = TravelMode,
  ##The variable from which our nests are determined
  alt.var = 'mode',
  #The variable that dictates the binary choice
  choice = 'choice',
  #List of nests as named vectors
  nests = list(fast = c('air','train'), slow = c('car','bus'))
  )

alt.var = 'mode'
This argument specifies the name of the variable in the dataset that contains the different alternatives (transportation modes in this case). Here, the alternatives are stored in the 'mode' variable.
choice = 'choice'
This argument specifies the name of the variable in the dataset that indicates whether an alternative was chosen (1) or not (0). In this case, the binary choice variable is called 'choice'.
nests = list(fast = c('air','train'), slow = c('car','bus'))
This argument defines the nests for the nested logit model. The nests are specified as a list of named vectors, where each vector contains the alternatives belonging to a particular nest. In this case, there are two nests: 'fast' (containing 'air' and 'train') and 'slow' (containing 'car' and 'bus').

The resulting nested_logit_model object can then be used to obtain various model statistics by calling the summary() function on it.

# The results
summary(nested_logit_model)

Call:
mlogit(formula = choice ~ gcost + wait, data = TravelMode, nests = list(fast = c("air",
    "train"), slow = c("car", "bus")), alt.var = "mode", choice = "choice")

Frequencies of alternatives:choice
    air   train     bus     car
0.27619 0.30000 0.14286 0.28095

bfgs method
15 iterations, 0h:0m:0s
g'(-H)^-1g = 2.04E-07
gradient close to zero

Coefficients :
                    Estimate Std. Error z-value  Pr(>|z|)
(Intercept):train -2.6632486  0.8797054 -3.0274  0.002466 **
(Intercept):bus   -2.9341306  0.9247620 -3.1728  0.001510 **
(Intercept):car   -8.0988987  1.8709536 -4.3288 1.500e-05 ***
gcost             -0.0234085  0.0059397 -3.9410 8.115e-05 ***
wait              -0.1499260  0.0364437 -4.1139 3.890e-05 ***
iv:fast            2.3918823  0.9701086  2.4656  0.013679 *
iv:slow            0.9745729  0.3598853  2.7080  0.006769 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Log-Likelihood: -189.74
McFadden R^2:  0.33132
Likelihood ratio test : chisq = 188.03 (p.value = < 2.22e-16)

Here is an interpretation of the results of the nested logit model:

Frequencies of alternatives
The frequencies show the proportion of each transportation mode selected in the dataset. In this case, air was chosen by 27.62% of the individuals, train by 30.00%, bus by 14.29%, and car by 28.10%. These values provide a baseline understanding of the popularity of each mode.
Coefficients
The coefficients represent the relationship between the predictor variables and the log odds of choosing a particular transportation mode relative to the reference category (in this case, the air mode). Positive coefficients indicate an increase in the log odds of choosing a mode, while negative coefficients indicate a decrease.
(Intercept):train, (Intercept):bus, and (Intercept):car
These are the alternative-specific constants for train, bus, and car, respectively. These represent the baseline log odds of choosing each mode relative to the air mode when all predictor variables are zero. The negative coefficients for all three alternatives indicate that the log odds of choosing each of these modes are lower than choosing air, given equal predictor variable values.
gcost
The generalized cost has a negative coefficient (-0.0234), which indicates that as the generalized cost of a transportation mode increases, the likelihood of choosing that mode decreases. This result is statistically significant, as indicated by the low p-value (8.115e-05).
wait
The waiting time also has a negative coefficient (-0.1499), meaning that as the waiting time for a transportation mode increases, the likelihood of choosing that mode decreases. This result is statistically significant as well, with a p-value of 3.890e-05.
Inclusive value (iv) parameters
The inclusive value parameters represent the dissimilarity of the alternatives within each nest. The positive and statistically significant coefficients for both the fast (iv:fast = 2.3919, p-value = 0.0137) and slow (iv:slow = 0.9746, p-value = 0.0068) nests indicate that the unobserved factors affecting the choice of alternatives within these nests are positively correlated.
Log-Likelihood
The log-likelihood value of -189.74 is a measure of how well the model fits the data. Higher values indicate a better fit.
McFadden R^2
The McFadden R^2 value of 0.3313 is a measure of the goodness-of-fit of the model. It ranges from 0 to 1, with higher values indicating a better fit. This value suggests that the model explains about 33.13% of the variation in the data.
Likelihood ratio test
The likelihood ratio test statistic (chisq = 188.03) and the p-value (< 2.22e-16) indicate that the model is statistically significant and an improvement over a model with no predictor variables.

Overall, the results of the nested logit model show that both generalized cost and waiting time negatively affect the choice of transportation mode, with individuals preferring lower-cost and shorter-wait alternatives. Additionally, the positive and significant inclusive value parameters suggest that there is a correlation between unobserved factors affecting the choice of alternatives within each nest (fast and slow transportation modes).