What is Computational Complexity Theory

Computational complexity theory is a branch of computer science that studies the computational resources needed to solve a given computational problem. These resources include time (how many steps it takes to solve a problem) and space (how much memory is required to solve the problem), but other measures of complexity can also be considered.

The primary objective of computational complexity theory is to classify problems based on their inherent difficulty. To do so, it defines complexity classes – sets of problems that can be solved using similar amounts of computational resources. Important complexity classes include P, NP and many others.

A central aspect of computational complexity theory is the study of intractable problems, problems for which no efficient solution is known. Through its exploration of these and other issues, computational complexity theory provides crucial insights into the limits of what computers can and cannot do, guiding the design of algorithms, the development of software, and the advancement of computing technology as a whole.

Time Complexity

Time complexity is a concept in computational complexity theory that represents the computational time taken by an algorithm to run, as a function of the size of the input to the program. It's one of the critical factors in determining the efficiency of an algorithm.

Big-O Notation

Big-O notation is a mathematical notation used to describe the upper bound, or worst-case scenario, of the time complexity of an algorithm. It describes how the running time of an algorithm grows with the size of the input. For example, an algorithm with a time complexity of O(n) would see its running time increase linearly with the input size.

O(1): Constant Time Complexity

An algorithm is said to have a constant time complexity when it is not dependent on the input size. No matter how large your input is, the time for computation will remain constant.

Example

Accessing a specific element in an array. No matter how large the array, it only takes one step to read an array element if its index is known.

O(n): Linear Time Complexity

An algorithm is said to have a linear time complexity when the running time increases at most linearly with the size of the input data.

Example

A simple search function which iterates through an array to find a specific value would have a time complexity of O(n), because in the worst case, it needs to look at every element once.

O(log n): Logarithmic Time Complexity

Logarithmic time complexity is associated with algorithms that cut the problem size by a fraction with each step.

Example

Binary search is an algorithm with logarithmic time complexity, O(log n). Each step of a binary search algorithm halves the number of elements to search from, thus it takes logarithmically fewer steps to find the target.

O(n^2): Quadratic Time Complexity

An algorithm is said to have a quadratic time complexity when it needs to perform a process for each element, and that process involves another loop over the elements.

Example

Bubble sort is a typical example of algorithm with O(n^2) complexity. For each element in the array, bubble sort compares it with every other element.

O(2^n): Exponential Time Complexity

Exponential time complexity occurs when the growth doubles with each addition to the input data set. The growth curve of an O(2^n) function is exponential - starting off very shallow, then rising meteorically.

Example

The classic example of O(2^n) complexity is the recursive calculation of Fibonacci numbers. The naive recursive algorithm performs an excessive amount of duplicated computation, effectively doubling the amount of work for each increase in the input size

Space Complexity

Space complexity is another critical concept in computational complexity theory. It represents the amount of memory space an algorithm needs in relation to the size of the input. Just as with time complexity, understanding an algorithm's space complexity is vital in assessing its efficiency, especially in memory-constrained environments.

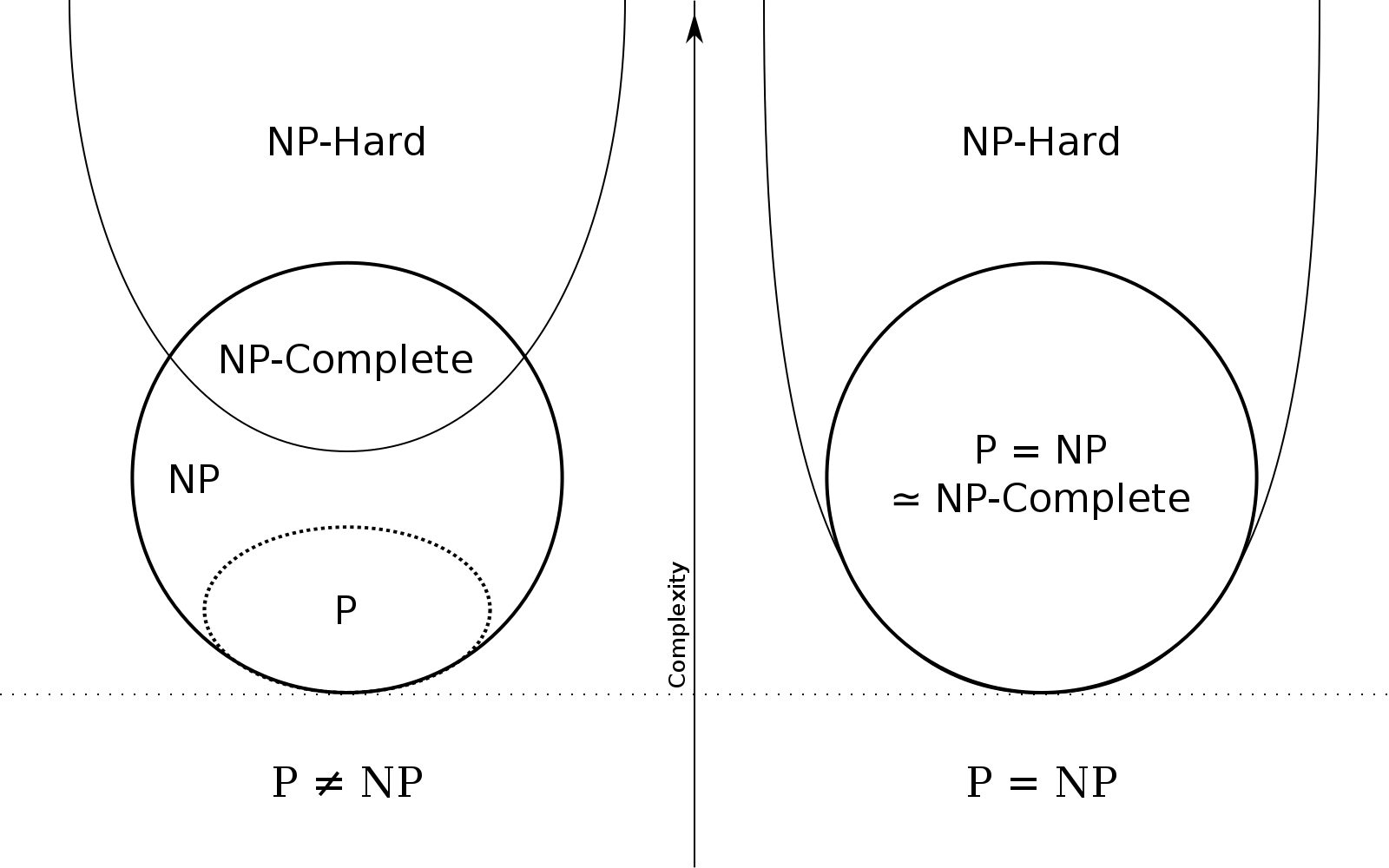
Complexity Classes

Complexity classes are a way to group computational problems that share similar resource-based characteristics. These characteristics often relate to the time or space required to solve the problem.

File:P np np-complete np-hard.svg

Class P

The class P (Polynomial Time) consists of decision problems that a deterministic Turing machine can solve in polynomial time. In Big O notation, this means that there is some polynomial p(n) so that the time complexity of solving the problem is O(p(n)).

For example, a problem that can be solved in O(n^2) time, where n is the size of the input, is in P. This means that as the input grows, the time it takes to solve the problem grows quadratically.

Class NP

The class NP contains problems for which a solution, once given, can be verified in polynomial time by a deterministic Turing machine. This is not the same as saying the problem can be solved in polynomial time. Rather, it means that if someone hands you a potential solution, you can check its correctness within polynomial time.

For example, if you have a potential solution to a problem and you can verify its correctness in O(n^3) time, that problem is in NP.

NP-Complete Problems

NP-Complete represents a set of problems to which any problem in NP can be reduced in polynomial time.

The NP-Complete class has two key properties:

• The problem itself is in NP. This means that if we're given a 'certificate', or a potential solution to the problem, we can verify the correctness of this solution in polynomial time.
• Any problem in NP can be reduced to it in polynomial time. In other words, a polynomial-time solution to this problem would allow us to solve all problems in NP in polynomial time.

NP-Hard Problems

NP-Hard is a class of problems that informally represents the "hardest" problems in NP (Nondeterministic Polynomial time), although they are not necessarily in NP themselves.

A problem is NP-Hard if every problem in NP can be reduced to it in polynomial time. This means that if you can solve an NP-Hard problem in polynomial time, you could solve all problems in NP within polynomial time as well.

It's important to note that while all NP-Complete problems are NP-Hard, not all NP-Hard problems are NP-Complete. The distinction here is that an NP-Hard problem doesn't have to be in NP itself, and it doesn't need to have a solution verifiable in polynomial time.

P versus NP Problem

The "P versus NP" problem is a fundamental question in computational complexity theory. It questions whether P (problems solvable in polynomial time) is the same as NP (problems whose solutions can be verified in polynomial time).

Significance of P versus NP

The P versus NP problem is not just a theoretical question; its answer holds significant practical implications. If it turns out that P = NP, it means that every problem for which we can verify a solution quickly, we can also solve quickly. This would revolutionize fields such as cryptography, optimization, database theory, AI, and much more.

On the other hand, if P ≠ NP, it means there are problems for which no fast algorithm can ever exist (assuming the solution needs to be correct for all inputs). This would confirm the security of many encryption algorithms, as the intractability of certain problems forms the foundation of modern cryptography.

State of the P versus NP Problem

Despite the efforts of many brilliant minds, the P versus NP problem remains unsolved and is considered one of the greatest open problems in computer science. In fact, it is one of the seven "Millennium Prize Problems" for which the Clay Mathematics Institute offers a $1 million prize for a correct solution.

The general belief in the computer science community is that P probably does not equal NP (P ≠ NP), mainly due to the lack of efficient algorithms for NP-complete problems. However, no one has been able to prove this conclusively.